-
(1).复数
 满足方程:
满足方程: ,则
,则 =
=(A).
 (B).
(B).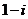 (C).
(C).
 (D).
(D).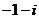
(2).已知集合
 ,R是实数集,则
,R是实数集,则 ( )
( )(A).
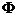 (B).R
(C).
(B).R
(C).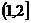 (D).
(D).

(3).右图表示一个几何体的三视图及相应数据,则该几何体的体积是 ( )
(A).
 (B).
(B).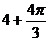 (C).
(C).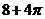 (D).
(D). 
(4).偶函数
 在区间[0,a](a>0)上是单调函数,且f(0).f(a)<0,
在区间[0,a](a>0)上是单调函数,且f(0).f(a)<0,则方程
 在区间[-a,a]内根的个数是 ( )
在区间[-a,a]内根的个数是 ( )(A). 3 (B). 2 (C). 1 (D). 0
(5).给出下面类比推理命题(其中Q为有理数集,R为实数集,C为复数集):
①“若a,b
 ”类比推出“若a,b
”类比推出“若a,b ”;
”;②“若a,b,c,d
 ”类比推出“若a,b,c,d
”类比推出“若a,b,c,d
则
 ”;
”;③“若a,b
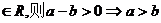 ” 类比推出“若a,b
” 类比推出“若a,b ”;
”;其中类比结论正确的个数是 ( )
(A).0 (B).1 (C).2 (D).3
 (6).函数
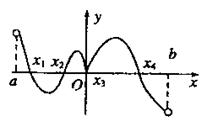
(6).函数 的定义域为(a,b),其导函数
的定义域为(a,b),其导函数 内的图象如图所示,
内的图象如图所示,则函数
 在区间(a,b)内极小值点的个数是( )
在区间(a,b)内极小值点的个数是( )(A).1 (B).2 (C).3 (D).4
(7).已知F1,F2分别是双曲线
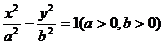 的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐用三角形,则该双曲线离心率的取值范围是( )
的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐用三角形,则该双曲线离心率的取值范围是( )(A).
 (B).
(B). (C).
(C).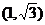 (D).
(D).
(8).2006年1月开始实施的《个人所得税法》规定:全月总收入不超过1600元的免征个人工资、薪金所得税,超过1600元的部分需征税,设全月总收入金额为x元,前三级税率如下表:
级数
全月应纳税金额
x-1600元
税率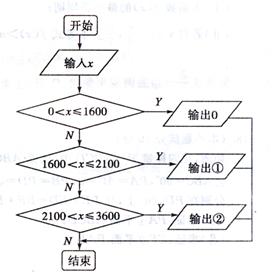
1
不超过500元部分
5%
2
超过500元至2000元部分
10%
3
超过2000元至5000元部分
15%
……
……
……
当全月总收入不超过3600元时,计算个人所得税的一个
算法框图如上所示,则输出①,输出②分别为 ( )
(A).0.05x,0.1x (B).0.05x, 0.1x-185
(C).0.05x-80, 0.1x (D).0.05x-80, 0.1x-185
-
(9).若
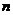 为等差数列
为等差数列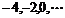 中的第8项,则二项式
中的第8项,则二项式 展开式中常数项是第 项.
展开式中常数项是第 项.(10).定义在R上的奇函数
 满足:对于任意
满足:对于任意 ,若
,若 ,
, __________.
__________.(11).定义
 是向量a和b的“向量积”,它的长度
是向量a和b的“向量积”,它的长度 为向量a和b的夹角,若
为向量a和b的夹角,若 =
.
=
.(12).有以下四个命题:
①两直线m,n与平面
 所成的角相等的充要条件是m//n;
所成的角相等的充要条件是m//n;②若
 ;
;③不等式
 上恒成立;
上恒成立;④设有四个函数
 ,其中在R上是增函数的函数有3个.
,其中在R上是增函数的函数有3个.其中真命题的序号是 .(漏填、多填或错填均不得分)
(13).(坐标系与参数方程选做题)已知极坐标系的极点
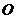 与直角坐标系的原点重合,极轴与
与直角坐标系的原点重合,极轴与 轴的正半轴重合,线
轴的正半轴重合,线 与线
与线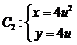 (参数
(参数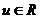 )交于
)交于 、
、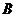 两点.
两点.写出
 的外接圆的标准方程
.
的外接圆的标准方程
.(14).(不等式选讲选做题)
已知方程
 的两根分别为1和2,则不等式
的两根分别为1和2,则不等式 的解集为 (用区间表示).
的解集为 (用区间表示).  (15).(几何证明选讲选做题)从⊙
(15).(几何证明选讲选做题)从⊙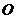 外一点
外一点 向圆引两条切线
向圆引两条切线 、
、 (
( 、
、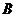 为切点)和割线
为切点)和割线
 与⊙
与⊙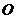 交于
交于 、
、 两点
两点 从
从 点作弦
点作弦 平行于
平行于 ,连结
,连结 交
交 于
于 ,连结
,连结 ,若
,若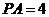 ,
,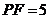 ,则
,则 .
. -
(16).(本小题满分12分)
 如图,在△ABC中,角A、B、C的对边分别为
如图,在△ABC中,角A、B、C的对边分别为 、
、 、c,
、c,且8
 =7
=7 ,
, ,AB边上的高CM长为
,AB边上的高CM长为 .
.
(Ⅰ)求
 的值;
(Ⅱ)求△ABC的面积
的值;
(Ⅱ)求△ABC的面积(17).(本小题满分12分)
设数列
 的前
的前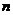 项和为
项和为 ,且
,且 ;数列
;数列 为等差数列,且
为等差数列,且 ,
, .
.(Ⅰ)求数列
 的通项公式;
的通项公式;(Ⅱ)若
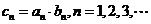 ,
,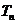 为数列
为数列 的前
的前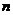 项和. 求证:
项和. 求证: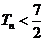 .
.(18).(本小题满分14分)
有10张形状、大小相同的卡片,其中2张上写着数字
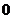 ,另外5张上写着数字1,余下3张上写着数字2。从中随机地取出1张,记下它的数字后放回原处。当这种手续重复进行2次时,
,另外5张上写着数字1,余下3张上写着数字2。从中随机地取出1张,记下它的数字后放回原处。当这种手续重复进行2次时, 为所记下的两个数之和。
为所记下的两个数之和。(Ⅰ)求
 =2时的概率;
(Ⅱ)求
=2时的概率;
(Ⅱ)求 的数学期望;
的数学期望;(19).(本小题满分14分)
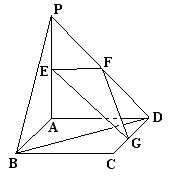 如图,平面
如图,平面 ⊥平面
⊥平面 ,
, 为正方形,
为正方形, ,
,且
 分别是线段
分别是线段 的中点。
的中点。(Ⅰ)求证:
 //平面
//平面 ;
; (Ⅱ)求异面直线
 与
与 所成的角;
所成的角;(Ⅲ)在线段
 上是否存在一点
上是否存在一点 ,使得点
,使得点 到平面
到平面 的距离为
的距离为 ;
;若存在,求出
 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。(20).(本小题满分14分)
已知椭圆
 的离心率为
的离心率为 ,直线
,直线 :
: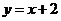 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆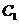 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.(Ⅰ)求椭圆
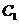 的方程;
的方程;(Ⅱ)设椭圆
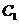 的左焦点为
的左焦点为 ,右焦点
,右焦点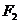 ,直线
,直线 过点
过点 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线 垂直
垂直 于点
于点 ,线段
,线段 垂直平分线交
垂直平分线交 于点
于点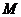 ,求点
,求点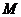 的轨迹
的轨迹 的方程;
的方程;(Ⅲ)设 (Ⅱ) 中的
 与
与 轴交于点
轴交于点 ,不同的两点
,不同的两点 在
在 上,且满足
上,且满足 求
求 的取值范围.
的取值范围.(21).(本小题满分14分)
已知
 、b为函数
、b为函数 的极值点
的极值点
(Ⅰ)求证:
 ;
;(Ⅱ)判断函数
 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;(Ⅲ)若曲线
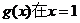 处的切线斜率为-4,且方程
处的切线斜率为-4,且方程 有两个不等的实根,求实数
有两个不等的实根,求实数 的取值范围.
的取值范围.
08年高考数学教学质量检测 数 学 试 题(理科) 2008.02.28 本试卷分选择题和非选择题两部分,共4页. 满分150分. 考试时间120分钟.参考答案
参考答案
一.选择题:每小题5分,满分40分.
|
题
号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
答 案 |
C |
D |
A |
B |
C |
A |
B |
D |
二.填空题:每小题5分,满分30分.(其中13~15题只能选做二题)
(9) [9]
(10) [0] (11) [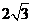 ]
(12) ②③
]
(12) ②③
(13)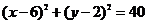 (14) [
(14) [ ]
(15) [6]
]
(15) [6]
三.解答题:本大题共6小题,满分80分.
 (16).[解](Ⅰ) ∵
(16).[解](Ⅰ) ∵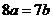 ,故设
,故设 =7k,b=8k(k>0),由余弦定理可
=7k,b=8k(k>0),由余弦定理可 =(72+82 -2×7×8cos1200)k2=169k2,∴c=13k,因此
=(72+82 -2×7×8cos1200)k2=169k2,∴c=13k,因此 ……………………(6分)
……………………(6分)
(Ⅱ)∵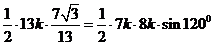 ∴
∴
∴ ……………………………………………………(12分)
……………………………………………………(12分)
(17).[解](Ⅰ)由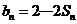 ,令
,令 ,则
,则 ,又
,又 ,所以
,所以 .
.
 ,则
,则 .…………………………………2分
.…………………………………2分
当 时,由
时,由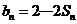 ,可得
,可得 .
.
即 . ………3分
. ………3分
所以 是以
是以 为首项,
为首项, 为公比的等比数列,于是
为公比的等比数列,于是 .……………4分
.……………4分
(Ⅱ)数列 为等差数列,公差
为等差数列,公差 ,可得
,可得 .…………6分
.…………6分
从而 . ………………………7分
. ………………………7分
∴

∴ . ……………10分
. ……………10分
从而 .
………………………12分
.
………………………12分
(17).[解](Ⅰ) 卡片的出法有(0,0),(0,1),(1,0),(0,2),(2,0),(1,1),(1,2),(2,1),(2,2)共9种
而 =2时,出现三种(0,2),(2,0),(1,1)
=2时,出现三种(0,2),(2,0),(1,1)
故 ………………………(7分)
………………………(7分)
(Ⅱ)同(Ⅰ)处理方法可求  ,
,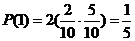 ,
,
 ,
,
因此, 的数学期望
的数学期望 ……(14分)
……(14分)
(18).[解]法一:(Ⅰ)证明:取AB中点H,连结GH,HE,
∵E,F,G分别是线段PA、PD、CD的中点,
∴GH//AD//EF,
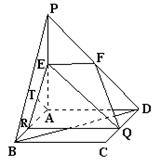 ∴E,F,G,H四点共面。………………1分
∴E,F,G,H四点共面。………………1分
又H为AB中点,
∴EH//PB。…………2分
又 面EFG,
面EFG, 平面EFG,
平面EFG,
∴PB//面EFG。…………3分
(Ⅱ)取BC的中点M,连结GM、AM、EM,则GM//BD,
∴∠EGM(或其补角)就是异面直线EG与BD所成的角。… 4分
在Rt△MAE中, ,
,
同理 ,又
,又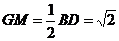 ,
,
∴在Rt△MGE中,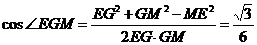 ……………………7分
……………………7分
故异面直线EG与BD所成的角为 。……………………………………8分
。……………………………………8分
(Ⅲ)假设在线段CD上存在一点Q满足题设条件。过点Q作QR⊥AB于R,连结RE,则QR//AD。
∵ABCD是正方形,△PAD是直角三角形,且PA=AD=2,
∴AD⊥AB,AD⊥PA,
又 ,
,
∴AD⊥平面PAB。
又∵E,F分别是PA,PD中点,
∴EF//AD,∴EF⊥平面PAB
又 面EFQ,
面EFQ,
∴面EFQ⊥平面PAB。
过A作AT⊥ER于T,则AT⊥面EFQ,
∴AT就是点A到平面EFQ的距离。……………………12分
设 ,则
,则 ,
, ,AE=1,
,AE=1,
在Rt△EAR中,
 解得
解得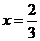 。
。
故存在点Q,当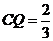 时,点A到平面EFQ的距离为
时,点A到平面EFQ的距离为 ……14分
……14分
解法二:建立如图所示的空间直角坐标系A-xyz,
则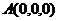 ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, 。
。
(Ⅰ)∵ ,
, ,
, ,……………………1分
,……………………1分
设 ,即
,即 解得
解得 。
。
∴ ,又∵
,又∵ 与
与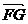 不共线,∴
不共线,∴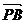 、
、 与
与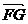 共面。……2分
共面。……2分
∵ 平面EFG,∴PB//平面EFG。………………3分
平面EFG,∴PB//平面EFG。………………3分
(Ⅱ)∵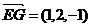 ,
, ,……………………4分
,……………………4分
∴ 。
。
故异面直线EG与BD所成的角为 。………………………8分
。………………………8分
(Ⅲ)假设在线段CD上存在一点Q满足题设条件。令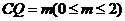 ,则
,则 ,
,
∴点Q的坐标为 ,∴
,∴ 。
。
而 ,设平面EFQ的法向量为
,设平面EFQ的法向量为 ,则
,则
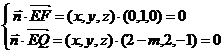 ∴
∴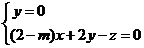 。
。
令 ,则
,则 。…………………………10分
。…………………………10分
又 ,∴点A到平面EFQ的距离
,∴点A到平面EFQ的距离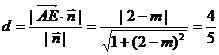 …………13分
…………13分
即 ,∴
,∴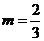 或
或 不合题意,舍去。
不合题意,舍去。
故存在点Q,当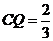 时,点A到平面EFQ的距离为
时,点A到平面EFQ的距离为 ………………14分
………………14分
(19).[解](Ⅰ) ∵ ……1分
……1分
∵直线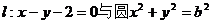 相切,
相切,
∴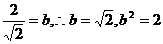 …………2分
…………2分
∴ …………3分
…………3分
∵椭圆C1的方程是  ………………4分
………………4分
(Ⅱ)∵MP=MF2,
∴动点M到定直线 的距离等于它到定点F1(1,0)的距离,
的距离等于它到定点F1(1,0)的距离,
∴动点M的轨迹是C为l1准线,F2为焦点的抛物线 ………………6分
∴点M的轨迹C2的方程为  …………7分
…………7分
(Ⅲ)Q(0,0),设 …………8分
…………8分
∴ …………9分
…………9分
∵
∴
∵ ,化简得
,化简得
∴ ………………11分
………………11分
∴
当且仅当  时等号成立 …………13分
时等号成立 …………13分
∵
∴当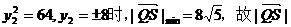 的取值范围是
的取值范围是 ……14分
……14分
(20).[解](Ⅰ) 依题设方程 的两根分别为
的两根分别为 ………2分,由题意可知:
………2分,由题意可知: 即
即 ………3分
………3分
则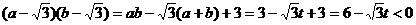
即 ……………4分
……………4分
(Ⅱ)由(Ⅰ):

(Ⅲ)由 ,
,
 的变化情况如下:
的变化情况如下:
|
|
(-∞,-3) |
-3 |
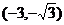 |
 |
-1 |
(-1,0) |
0 |
 |
- |
0 |
+ |
+ |
0 |
- |
|
 |
  |
极小值 |
 |
 |
极大值 -1 |
 |
 |
|
 ………………13分
………………13分

 ………………14分
………………14分
