-
1.已知集合A=
 ,集合B=
,集合B= ,则
,则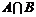 =( )
=( )A.
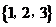 B.
B. C.
C. D.
D.
-
2.函数
 的反函数解析式为( )
的反函数解析式为( )A.
 (
( ) B.
) B.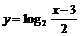 (
( )
) C.
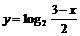 (
( )
D.
)
D. (
( )
) -
3.已知
 、
、 是不同的两个平面,直线
是不同的两个平面,直线 ,直线
,直线 ,命题
,命题 :
: 与
与 没有公共点;命题
没有公共点;命题 :
: ,则
,则 是
是 的(
)
的(
)A.充分不必要的条件 B.必要不充分的条件 C.充要条件 D.既不充分也不必要的条件
-
4.若函数
 图象的一条对称轴为
图象的一条对称轴为 ,且
,且 ,则实数
,则实数 的值等于( )
的值等于( )A.±1 B.±3 C.-3或1 D.-1或3
-
5.若函数
 的图象的顶点在第四象限,则其导函数
的图象的顶点在第四象限,则其导函数 的图象可能是(
)
的图象可能是(
)
-
6.某公司租地建仓库,每月土地租用费
 与仓库到车站的距离成反比,而每月库存货物的运费
与仓库到车站的距离成反比,而每月库存货物的运费 与仓库到车站的距离成正比。如果要在距离车站10km处建仓库,这两项的费用
与仓库到车站的距离成正比。如果要在距离车站10km处建仓库,这两项的费用 、
、 分别为2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站(
)
分别为2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站(
)A.5km处 B.4km处 C.3km处 D.2km处
-
7.已知抛物线
 的准线与双曲线
的准线与双曲线 的一条准线重合,则这条抛物线
的一条准线重合,则这条抛物线 与双曲线
与双曲线 的交点P到抛物线焦点的距离为( )
的交点P到抛物线焦点的距离为( )A.
 B.21 C.6
D.4
B.21 C.6
D.4 -
8.有两排座位,前排6个座位,后排7个座位,现安排2人就座,规定这2人不左右相邻,那么不同的坐法种数是( )
A.92 B.102 C.132 D.134
-
9.已知直线
 按向量
按向量 平移后得到的直线
平移后得到的直线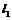 与圆
与圆 相切,那么
相切,那么 的值为(
)
的值为(
) A.9或-1 B.5或-5 C.-7或7 D.-1或9
-
10.在R上定义运算
 :
: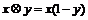 ,若不等式
,若不等式 对任意实数
对任意实数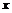 都成立,则实数
都成立,则实数 的取值范围是(
)
的取值范围是(
)A.
 B.
B. C.
C. D.
D. 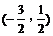
-
11.当
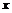 、
、 满足条件
满足条件 时,变量
时,变量 的取值范围是( )
的取值范围是( )A.
 B.
B. C.
C. D.
D. 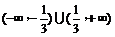
-
12.如果数列
 满足
满足 ,
, ,且
,且 (
( ≥2),则这个数列的第10项等于(
)
≥2),则这个数列的第10项等于(
)A.
 B.
B. C.
C. D.
D.
-
把答案填写在答题卷上相应的位置。只须写出最后结果,不必写出解题过程。
13.
 已知平面上三点A、B、C满足
已知平面上三点A、B、C满足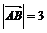 ,
, ,
, ,则
,则 的值等于
。
的值等于
。 -
14.在
 展开式中,含
展开式中,含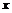 的负整数指数幂的项共有
项.
的负整数指数幂的项共有
项. -
15.如图,正方形ABCD中,E、F分别是AB、AD的中点,将此正方形沿
EF折成直二面角后,异面直线AF与BE所成角的余弦值为 .
-
16.设函数
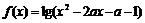 ,给出如下命题:
,给出如下命题:①无论
 取何实数,函数
取何实数,函数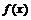 的值域都是R;②函数
的值域都是R;②函数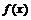 必有最小值;③若
必有最小值;③若 ,且
,且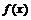 的定义域为
的定义域为 ,则函数
,则函数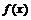 有反函数;④对于任意实数
有反函数;④对于任意实数 ,一定有
,一定有 ,
,其中正确命题的序号是 。(将你认为正确的命题的序号都填上)
草 稿 纸
-----------------------------------------------------------------------------------
-
17.(12分)已知函数
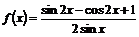 .
.⑴求
 的定义域;
的定义域;⑵设
 为任意角,且
为任意角,且 ,求
,求 的值。
的值。 -
18.(12分)已知
 ,等差数列
,等差数列 中,
中, ;
;⑴求实数
 的值;
的值;⑵求数列
 的通项公式;
的通项公式;⑶求
 的值;
的值; -
19.(12分)某汽车驾驶学校在学员结业前,对学员的驾驶技术进行4次考核,规定:学员必须按顺序从第一次开始参加考核,一旦考核合格就不必参加以后的考核,否则还需参加下次考核。若学员小李参加每次考核合格的概率依次组成一个公差为
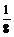 的等差数列,他参加第一次考核合格的概率不超过
的等差数列,他参加第一次考核合格的概率不超过 ,且他直到参加第二次考核才合格的概率为
,且他直到参加第二次考核才合格的概率为 。
。⑴求小李第一次参加考核就合格的概率
 ;
;⑵求小李第四次参加考核的概率。
-
20.
 (12分)在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
(12分)在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB= ,EF=EC=1,
,EF=EC=1, ⑴求证:平面BEF⊥平面DEF;
⑵求二面角A-BF-E的大小。
-
21.(12分)已知二次函数
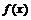 的二次项系数为
的二次项系数为 ,且不等式
,且不等式 的解集为
的解集为

⑴若方程
 有两个相等的实数根,求
有两个相等的实数根,求 的解析式;
的解析式;⑵若函数
 无极值,求实数
无极值,求实数 的取值范围
的取值范围 -
22.(14分)已知方向向量为
 的直线
的直线 过椭圆C:
过椭圆C: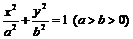 的焦点以及点(0,
的焦点以及点(0, ),椭圆C的中心关于直线
),椭圆C的中心关于直线 的对称点在椭圆C的右准线上。
的对称点在椭圆C的右准线上。⑴求椭圆C的方程。
⑵是否存在过点E(-2,0)的直线
 交椭圆C于点M、N,使⊿MON的面积为
交椭圆C于点M、N,使⊿MON的面积为 ,(O为坐标原点)?若存在,求出直线
,(O为坐标原点)?若存在,求出直线 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
08届高考文科数学第二次模拟测试试题参考答案
20
21
22
数学(文科)试题参考答案及评分标准
一、选择题:
1.A 2.D 3.B 4.C 5.C 6.A 7.D 8.D 9.A 10.C 11.B 12.D
二、填空题:13.-25; 14.4 15. ; 16.①③
; 16.①③
三、解答题:
17.解:⑴由 得
得 (
( ),所以
),所以 的定义域是
的定义域是 ;……(4分)
;……(4分)
⑵由 得
得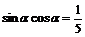 , ………………………(6分)
, ………………………(6分)
∵ 为任意角,
为任意角,
∴ ………………………(10分)
………………………(10分)
 .
………………………(12分)
.
………………………(12分)
18.⑴解:∵ ,∴
,∴ ,
, ……(2分)
……(2分)
由 得
得 ,化简得
,化简得  ,
,
∴ .
………………………(4分)
.
………………………(4分)
⑵当 时,
时, ;当
;当 时,
时, .……………………(8分)
.……………………(8分)
⑶当 时,
时, ;…………………(10分)
;…………………(10分)
当 时,
时, .………………………………(12分)
.………………………………(12分)
19.解:⑴根据题意,得  ,解得
,解得 或
或 .
.
∵ ,∴
,∴ ,即小李第一次参加考核就合格的概率为
,即小李第一次参加考核就合格的概率为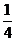 .……………(6分)
.……………(6分)
⑵由⑴的结论知,小李四次考核每次合格的概率依次为 ……………(8分)
……………(8分)
∴小李第四次参加考核的概率为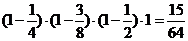 .……………(12分)
.……………(12分)
20.⑴解法1: ①证明: ∵平面ACEF⊥平面ABCD,EC⊥AC,∴EC⊥平面ABCD.
连接BD交AC于点O,连接FO.
 ∵正方形ABCD的边长为
∵正方形ABCD的边长为 ,∴AC=BD=2.
,∴AC=BD=2.
在直角梯形ACEF中,∵EF=EC=1,O为AC中点,
∴FO∥EC,且FO=1;易求得DF=BF= ,DE=BE=
,DE=BE= .
.
由勾股定理知 DF⊥EF,BF⊥EF,
∴∠BFD是二面角B-EF-D的平面角.
由BF=DF= ,BD=2可知∠BFD=
,BD=2可知∠BFD= ,
,
∴平面BEF⊥平面DEF ……………………(6分)
⑵取BF中点M,BE中点N,连接AM、MN、AN,∵AB=BF=AF= ,∴AM⊥BF.
,∴AM⊥BF.
又∵MN∥EF,EF⊥BF,∴MN⊥BF,
∴∠AMN就是二面角A-BF-E的平面角。
易求得 ,
,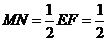 .取BC中点P,连接NP,则NP∥EC,
.取BC中点P,连接NP,则NP∥EC,
∴NP⊥平面ABCD,连接AP,在Rt△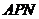 中,可求得
中,可求得 ,
,
∴在△ 中,由余弦定理求得
中,由余弦定理求得 ,∴
,∴ .
.
 即二面角A-BF-E的大小为
即二面角A-BF-E的大小为 …………(12分)
…………(12分)
解法2:⑴∵平面ACEF⊥平面ABCD,EC⊥AC,∴EC⊥平面ABCD.
建立如图所示的空间直角坐标系C-xyz,则 ,
,
 ,
, ,
, ,
, ,
,
∴ ,
, ,
,
………………(2分)
设平面BEF、平面DEF的法向量分别为 ,则
,则
 ①
①
 ②,
②,
 ③,
③,
 ④.
④.
由①③③④解得 ,
,
∴ ,………………(4分)
,………………(4分)
∴ ,∴
,∴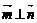 ,故平面BEF⊥平面DEF.…………(6分)
,故平面BEF⊥平面DEF.…………(6分)
⑵设平面ABF的法向量为 ,∵
,∵ ,
,
∴ ,
, ,解得
,解得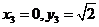
∴ ,………(8分)∴
,………(8分)∴ ………………(10分)
………………(10分)
由图知,二面角A-BF-E的平面角是钝角,故所求二面角的大小为 …(12分)
…(12分)
21.解:⑴设
 ,∵不等式
,∵不等式 的解集为
的解集为

∴ ……… ①
……… ①  ……… ②
……… ②
又∵ 有两等根,
有两等根,
∴ ……… ③
……… ③
由①②③解得
 ………………………………………(5分)
………………………………………(5分)
又∵ ,∴
,∴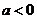 ,故
,故 .
.
∴ ……………………………………………(7分)
……………………………………………(7分)
⑵由①②得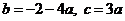 ,∴
,∴ ,
,
 …………………………………………(9分)
…………………………………………(9分)
∵ 无极值,∴方程
无极值,∴方程
 ,解得
,解得 ………………(12分)
………………(12分)
22.解:⑴直线 ①,过原点垂直于
①,过原点垂直于 的直线方程为
的直线方程为 ②
②
解①②得 .
.
∵椭圆中心O(0,0)关于直线 的对称点在椭圆C的右准线上,
的对称点在椭圆C的右准线上,
∴ ,
………(3分)
,
………(3分)
∵直线 过椭圆焦点,∴该焦点坐标为(2,0),
过椭圆焦点,∴该焦点坐标为(2,0),
∴ ,故椭圆C的方程为
,故椭圆C的方程为 ③……………(6分)
③……………(6分)
⑵当直线 的斜率存在时,设
的斜率存在时,设 代入③并整理得
代入③并整理得
 ,
,
设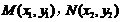 ,则
,则 …………………(8分)
…………………(8分)
∴ ,………(10分)
,………(10分)
点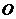 到直线
到直线 的距离
的距离  , ……………………………………(11分)
, ……………………………………(11分)
∵ , ∴
, ∴ ,即
,即
解得  ,此时
,此时 …………………………………(13分)
…………………………………(13分)
当直线 的斜率不存在时,
的斜率不存在时,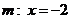 ,也有
,也有
故存在直线 满足题意,其方程为
满足题意,其方程为 .……………(14分)
.……………(14分)