高中毕业班数学教学质量检测
数
学(文) 试 题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
参考公式：
如果事件A、B互斥，那么
球的表面积和体积公式
P(A+B)=P(A)+P(B)
锥体的体积公式
S=4 V球=
其中S和h分别表示底面积和高
-
1．复数
为虚数单位)等于 ( )A．1 B．－1 C．i D．－i
-
2．函数
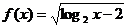的定义域是 ( )A．(3，+∞) B．(4，+∞) C．
D．
-
3．在下列直线中，是圆
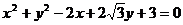的切线的是 ( )A．x=0 B．y=0 C．x=y D．x=－y
-
4．已知
的最小值是 ( )A．9 B．4 C．3 D．2
5．函数20070319
的值域是 ( )
A．
B．
C．(－∞，0) D．(0，+∞) 
6．已知正方体的外接球的体积是
则这个正方体的棱长是( )
A．
B．
C．
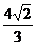D．
-
7．右面框图表示的程序所输出的结果是( )
A．11 B．12
C．132 D．1320
-
8．设
，那么“
”是“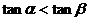
”的 ( )A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分也不必要条件
-
9．已知直线m，n，平面
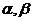，下列命题中正确的是 ( )A．
B．
C．
D．
-
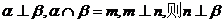
10．下列直线中，是抛物线
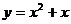过点(－1，0)的切线的是 ( )A．
B．
C．
D．
-
11．设
( )A．
B．
C．
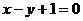D．
-
12．要得到函数
的图象，只须将函数
的图象 ( )A．向左移
个单位，再把所有点的横坐标伸长到原来的2倍，纵坐标不变B．向右移
个单位，再把所有点的横坐标伸长到原来的2倍，纵坐标不变C．向左移
个单位，再把所有点的横坐标缩短到原来的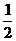
倍，纵坐标不变D．向右移
个单位，再把所有点的横坐标缩短到原来的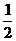倍，纵坐标不变 -
13．数据5，7，7，8，10，11的标准差是 .
14．从含有两件正品a1，a2和一件次品b1的3件产品中每次任取1件，每次取出后不放回，连续取两次，则取出的两件产品中恰有一件次品的概率是
. -
15．双曲线
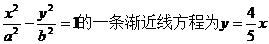，则双曲线的离心率为 .
-
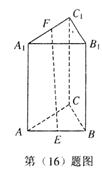
16．如图，正三棱柱ABC-A1B1C1的底边长为2，
侧棱长为4，E、F分别是AB、A1C1的中点，
则EF的长等于 .
-
17．(本小题满分12分)
已知向量
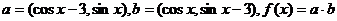
(Ⅰ)若
的单调增区间；
(Ⅱ)若20070319
的值.
-
18．(本小题满分12分)
已知函数
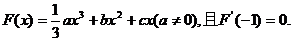
(Ⅰ)若F(x)在x=1处取得极小值－2，求函数F(x)的单调区间；
(Ⅱ)令
的解集为A，且满足A∪(0，1)=(0，+∞)，求
的取值范围. -
19．(本小题满分12分)
如图，在棱长为2的正方体ABCD-A1B1C1D1中，E、F分别为BD、BB1的中点，
(Ⅰ)求证：EF⊥AD1；
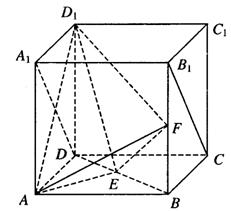(Ⅱ)求二面角E-D1F-A的大小；(Ⅲ)求三棱锥D1-AEF的体积.
-
20．(本小题满分12分)
某加工厂需定期购买原材料，已知每公斤原材料的价格为1.5元，每次购买原材料需支付运费600元.每公斤原材料每天的保管费用为0.03元，该厂每天需要消耗原材料400公斤，每次购买的原材料当天即开始使用(即有400公斤不需要保管).
(Ⅰ)设该厂每x天购买一次原材料，试写出每次购买的原材料在x天内总的保管费用y1关于关于x的函数关系式；
(Ⅱ)求该厂多少天购买一次原材料才能使平均每天支付的总费用y最少，并求出这个最少(小)值；
-
21．(本小题满分12分)
已知数列{an}满足a1=1，a2=－13，
(Ⅰ)设
的通项公式；(Ⅱ)求n为何值时，
最小(不需要求的最小值) -
22．(本小题满分14分)
已知椭圆
一个顶点为A(0，1)，且它的离心率与双曲线
的离心率互为倒数.(I)求椭圆的方程；
(Ⅱ)过A点且斜率为k的直线与椭圆相交于A、B两点，点M在椭圆上，并且满足
高中毕业班数学教学质量检测 数 学(文) 试 题 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟. 第Ⅰ卷(选择题 共60分) 参考公式： 如果事件A、B互斥，那么 球的表面积和体积公式 P(A+B)=P(A)+P(B) 锥体的体积公式 S=4 V球= 其中S和h分别表示底面积和高 参考答案
，求k的值.
参考答案
一、选择题(本大题共12小题，每小题5分，共60分)
CDACD DDCCD BC
二、填空题(本大题共4小题，每小题4分，共16分)
13．2
14．
15．
16．
三、解答题
17．(本小题满分12分)
解：(I)
…………………………3分
由
又
……………………6分
(Ⅱ)由(I)知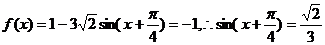
………………………………………………12分
18．(本小题满分12分)
解：(I)
①
又由在x=1处取得极小值－2可知
③
将①、②、③式联立，解得a=3，b=0，c=－3
……………………………………4分
由
同理，由
∴F(x)的单调递减区间为[－1，1]，单调递增区间为
……6分
(Ⅱ)由上问知：
又
…………………………8分
∴当a＜0时，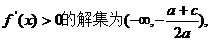
显然A∪(0，1)=(0，+∞)不成立，不满足题意。∴a＞0，且
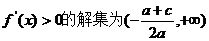……………………10分
又由A∪(0，1)=(0，+∞)知：
……12分
19．(本小题满分12分)
解：(I)连结B1D、A1D
∵ABCD-A1B1C1D1是正方体，
|
∴A1D⊥B1D(三垂线定理).
又∵在△BB1D内，E、F分别为BD、BB1的中点，
∴EF//B1D
∴EF⊥AD1………………………………4分
(Ⅱ)以A为原点，AB、AD、AA1分别为x、y、z轴，建立空间直角坐标系，则易知各点的坐标分别为：A(0，0，0)E(1，1，0)F(2，0，1)D1(0，1，2)
………………………………6分
∵AE⊥平面BB1D1D，∴
就是平面BB1D1D的法向量.
设平面AFD1的法向量n=(x，y，z)，则
令x=1得z=－2，y=2即n=(1，2，-2)，
由图形可知，二面角E-D1F-A的平面角为锐角，
∴二面角E-D1F-A的大小为45°…………………………8分
(Ⅲ)由(I)知，EF⊥AD1，又显然EF⊥AE，∴EF⊥平面AED1
∴EF就是三棱锥F-AED1的高，
又∵AE⊥平面BB1D1D，
∴AE⊥D1E
∴三棱锥F-AED1的底面AED1是直角三角形…………………………10分
易求得
∴三棱锥D1-AEF的体积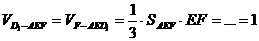
…………12分
20．(本小题满分12分)
解：(I)每次购买原材料后，当天用掉的400公斤原材料不需要保管费，第二天用掉的400公斤原材料需保管1天，第三天用掉的400公斤原材料需保管2天，第四天用掉的400公斤原材料需保管3天，……第x天(也就是下次购买原材料的前一天)用掉最后的400公斤原材料需保管x－1天.
∴每次购买的原材料在x天内总的保管费用
(元)……………………6分
(Ⅱ)由上问可知，购买依次原材料的总的费用为
元，
∴购买依次原材料平均每天支付的总费用
∴
取等号.
∴该厂10天购买依次原材料可以使平均每天支付的总费用y最少，为714元.……12分
21．(本小题满分12分)
解：(I)
2分
即数列{bn}的通项公式为
…………………………6分
(Ⅱ)若an最小，则
…………9分
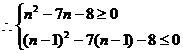注意n是正整数，解得8≤n≤9
∴当n=8或n=9时，an的值相等并最小……………………………………12分
22．(本小题满分14分)
解：(Ⅰ)∵双曲线
∴椭圆的离心率为
。………………………………2分
∵椭圆
的一个顶点为A(0，1)，∴b=1
…………4分
(Ⅱ)过A点且斜率为k的直线的方程是y=kx+1，代入到椭圆方程中，消去y并整理得
…………………………………………………………6分
显然这个方程有两解。设
即A(0，1)，B
……………………………………8分
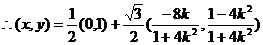
……………………10分
将E点的坐标代入到椭圆方程中，并去坟墓可得
展开整理得
………………………………14分
方法二：
(Ⅱ)过A点且斜率为k的直线的方程是y=kx+1，代入到椭圆方程中，消去y并整理得
①………………………………………………6分
显然这个方程有两解。设
∵点M在C上，
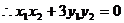…………………………………………12分
②
又由①式知：
代入到②式得
………………………………14分