-
1. 给出直线的方向向量
 或
或 ,等于已知直线的斜率
,等于已知直线的斜率 或
或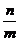 ;
; -
2. 给出
 与
与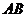 相交,等于已知
相交,等于已知 过
过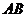 的中点;
的中点; -
3. 给出
 ,等于已知
,等于已知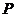 是
是 的中点;
的中点; -
4. 给出
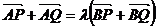 ,等于已知
,等于已知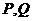 与
与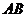 的中点三点共线;
的中点三点共线; -
5. 给出以下情形之一
①
 ,
,②存在实数

③若存在实数
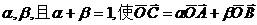 ,等于已知
,等于已知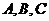 三点共线.
三点共线. -
6. 给出
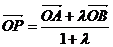 ,等于已知
,等于已知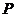 是
是 的定比分点,
的定比分点, 为定比,即
为定比,即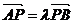
-
7. 给出
 ,等于已知
,等于已知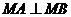 ,即
,即 是直角,给出
是直角,给出 ,等于已知
,等于已知 是钝角, 给出
是钝角, 给出 ,等于已知
,等于已知 是锐角,
是锐角, -
8. 给出
 ,等于已知
,等于已知 是
是 的平分线/
的平分线/ -
9. 在平行四边形
 中,给出
中,给出 ,等于已知
,等于已知 是菱形;
是菱形; -
10. 在平行四边形
 中,给出
中,给出 ,等于已知
,等于已知 是矩形;
是矩形; -
11. 在
 中,给出
中,给出 ,等于已知
,等于已知 是
是 的外心;
的外心; -
12. 在
 中,给出
中,给出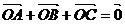 ,等于已知
,等于已知 是
是 的重心;
的重心; -
13. 在
 中,给出
中,给出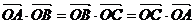 ,等于已知
,等于已知 是
是 的垂心;
的垂心; -
14. 在
 中,给出
中,给出

 等于已知
等于已知 通过
通过 的内心;
的内心; -
15. 在
 中,给出
中,给出 等于已知
等于已知 是
是 的内心;
的内心; -
16. 在
 中,给出
中,给出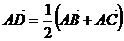 ,等于已知
,等于已知 是
是 中
中 边的中线;
边的中线; -
17. 给出
 ,等于已知
,等于已知 的面积
的面积 -
[例1](2005年.辽宁卷21)
已知椭圆
 的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足
的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足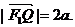 点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足
点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足
(Ⅰ)设
 为点P的横坐标,证明
为点P的横坐标,证明 ;
;(Ⅱ)求点T的轨迹C的方程;
(Ⅲ)试问:在点T的轨迹C上,是否存在点M使△F1MF2的面积S=
 若存在,求∠F1MF2 的正切值;若不存在,请说明理由.
若存在,求∠F1MF2 的正切值;若不存在,请说明理由.解 : (Ⅰ)证法一:设点P的坐标为

由P
 在椭圆上,得
在椭圆上,得
由
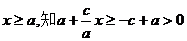 ,所以
,所以

证法二:设点P的坐标为
 记
记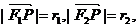
则

由

证法三:设点P的坐标为
 椭圆的左准线方程为
椭圆的左准线方程为
由椭圆第二定义得
 ,即
,即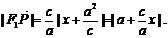
由
 ,所以
,所以
(Ⅱ)解法一:设点T的坐标为

当
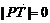 时,点(
时,点( ,0)和点(-
,0)和点(- ,0)在轨迹上.
,0)在轨迹上.当|
 时,由
时,由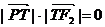 ,得
,得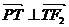 .
.又
 ,所以T为线段F2Q的中点.
,所以T为线段F2Q的中点.在△QF1F2中,
 ,所以有
,所以有
综上所述,点T的轨迹C的方程是

解法二:设点T的坐标为

当
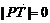 时,点(
时,点( ,0)和点(-
,0)和点(- ,0)在轨迹上.
,0)在轨迹上.当|
 时,由
时,由 ,得
,得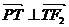 .
.又
 ,所以T为线段F2Q的中点.
,所以T为线段F2Q的中点. 设点Q的坐标为(
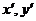 ),
),则

因此
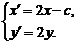 ①
①由
 得
得 ②
②将①代入②,可得

综上所述,点T的轨迹C的方程是

(Ⅲ)解法一:C上存在点M(③
④
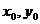 )使S=
)使S= 的充要条件是
的充要条件是
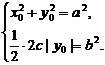
由③得
 ,由④得
,由④得 所以,当
所以,当 时,存在点M,使S=
时,存在点M,使S= ;
;当
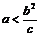 时,不存在满足条件的点M.
时,不存在满足条件的点M.当
 时,
时, ,
,由
 ,
,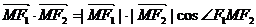 ,
, ,得
,得
解法二:C上存在点M(
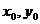 )使S=
)使S= 的充要条件是
的充要条件是③
④
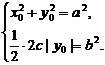
由④得
 上式代入③得
上式代入③得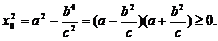
于是,当
 时,存在点M,使S=
时,存在点M,使S= ;
;当
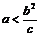 时,不存在满足条件的点M.
时,不存在满足条件的点M.当
 时,记
时,记 ,
,由
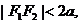 知
知 ,则
,则
[例2](2005年.重庆卷.理21)
已知椭圆C1的方程为
 ,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.
,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.(Ⅰ)求双曲线C2的方程;
(Ⅱ)若直线
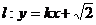 与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足
与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足 (其中O为原点),求k的取值范围.
(其中O为原点),求k的取值范围.解:(Ⅰ)设双曲线C2的方程为
 ,则
,则
故C2的方程为

(Ⅱ)将
 代入
代入 得
得
由直线l与椭圆C1恒有两个不同的交点得
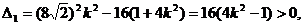
即
 ①
① .
.由直线l与双曲线C2恒有两个不同的交点A,B得


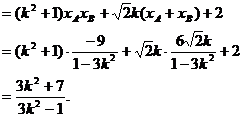
 解此不等式得
解此不等式得 ③
③由①、②、③得
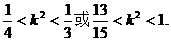
故k的取值范围为
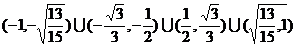
[例3](2005年.全国卷Ⅰ.理21文22)
已知椭圆的中心为坐标原点O,焦点在
 轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,
轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点, 与
与 共线.
共线.(I)求椭圆的离心率;
(II)设M为椭圆上任意一点,且
 ,证明
,证明 为定值.
为定值.解:(I)设椭圆方程为

则直线AB的方程为

化简得
 .
.令
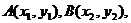
则


 共线,得
共线,得
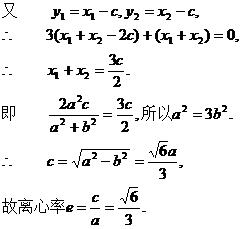
(II)证明:由(I)知
 ,所以椭圆
,所以椭圆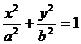 可化为
可化为 .
.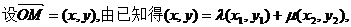

 在椭圆上,
在椭圆上,
即
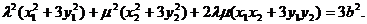 ①
①由(I)知
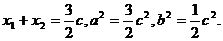


又
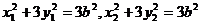 又,代入①得
又,代入①得 
故
 为定值,定值为1.
为定值,定值为1.