-
1. 如果
 的展开式中含有非零常数项,则正整数n的最小值为
的展开式中含有非零常数项,则正整数n的最小值为A.3 B.5 C.6 D.10
-
2.将
 的图象按向量a=
的图象按向量a=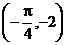 平移,则平移后所得图象的解析式为
平移,则平移后所得图象的解析式为A.
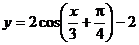 B.
B. 
C.
 D.
D.
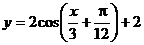
-
3.设P和Q是两个集合,定义集合P-Q=
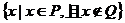 ,如果P={x|log2x<1},Q={x||x-2|<1},那么P-Q等于
,如果P={x|log2x<1},Q={x||x-2|<1},那么P-Q等于A.{x|0<x<1} B.{x|0<x≤1} C.{x|1≤x<2} D.{x|2≤x<3}
-
4.平面α外有两条直线m和n,如果m和n在平面α内的射影分别是m'和n',给出下列四个命题:
①m'⊥n'
 m⊥n;
②m⊥n
m⊥n;
②m⊥n m'⊥n'
m'⊥n'③m'与n'相交
 m与n相交或重合; ④m'与n'平行
m与n相交或重合; ④m'与n'平行 m与n平行或重合.
m与n平行或重合.其中不正确的命题个数是
A.1 B.2 C.3 D.4
-
5.已知p和q是两个不相等的正整数,且q≥2,则

A.0 B.1 C.
 D.
D.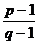
-
6.若数列{an}满足
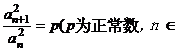 N*),则称{an}为“等方比数列”.
N*),则称{an}为“等方比数列”.甲:数列{an}是等方比数列;乙:数列{an}是等比数列.则
A. 甲是乙的充分条件但不是必要条件
B. 甲是乙的必要条件但不是充分条件
C. 甲是乙的充要条件
D. 甲既不是乙的充分条件也不是乙的必要条件
-
7.双曲线C1:
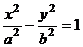 (a>0,b>0)的左准线为l,左焦点和右焦点分别为F1和F2;抛物线C2的准线为l,焦点为F2.C1和C2的一个交点为M,则
(a>0,b>0)的左准线为l,左焦点和右焦点分别为F1和F2;抛物线C2的准线为l,焦点为F2.C1和C2的一个交点为M,则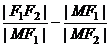 等于
等于A.-1 B.1 C.
 D.
D.
-
8.已知两个等差数列{an}和{bn}的前n项和分别为An和Bn,且
 ,则使得
,则使得 为整数的正整数n的个数是
为整数的正整数n的个数是A.2 B.3 C.4 D.5
-
9.连掷两次骰子得到的点数分别为m和n,记向量a=(m,n)与向量b=(1,-1)的夹角为θ,则
 的概率是
的概率是A.
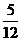 B.
B. C.
C.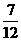 D
D
-
10.已知直线
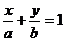 (a,b是非零常数)与圆x2+y2=100有公共点,且公共点的横坐标和纵坐标均为整数,那么这样的直线共有
(a,b是非零常数)与圆x2+y2=100有公共点,且公共点的横坐标和纵坐标均为整数,那么这样的直线共有A.60条 B.66条 C.72条 D.78条
-
11.已知函数y=2x-a 的反函数是y=bx+3,则 a= ;b= .
-
12.复数z=a+bi,a,b∈R,且b≠0,若z2-4bz是实数,则有序实数对(a,b)可以是 .(写出一个有序实数对即可)
-
13.设变量x,y满足约束条件
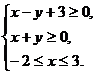 则目标函数2x+y的最小值为
.
则目标函数2x+y的最小值为
. -
14.某篮球运动员在三分线投球的命中率是
 ,他投球10次,恰好投进3个球的概率
.(用数值作答)
,他投球10次,恰好投进3个球的概率
.(用数值作答) -
15.
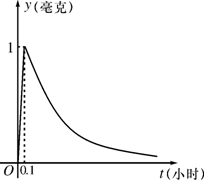 为了预防流感,某学校对教室用药熏消毒法进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为
为了预防流感,某学校对教室用药熏消毒法进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为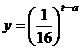 (a为常数),如图所示,根据图中提供的信息,回答下列问题:
(a为常数),如图所示,根据图中提供的信息,回答下列问题:(Ⅰ)从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为 .
(Ⅱ)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那从药物释放开始,至少需要经过 小时后,学生才能回到教室.
-
16.(本小题满分12分)
已知△ABC的面积为3,且满足0≤
 ≤6,设
≤6,设 和
和 的夹角为θ.
的夹角为θ.(Ⅰ)求θ的取值范围;
(Ⅱ)求函数f(θ)=2sin2
 的最大值与最小值.
的最大值与最小值.分 组
频 数

4

25

30

29
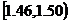
10
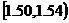
2
合 计
100
-
17.(本小题满分12分)
在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如右表:
(Ⅰ)在答题卡上完成频率分布表,并在给定的坐标系中画出频率分布直方图;
(Ⅱ)估计纤度落在
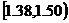 中的概率及纤度小于1.40的概率是多少;
中的概率及纤度小于1.40的概率是多少;(Ⅲ)统计方法中,同一组数据常用该组区间的中点值(例如区间
 的中点值是1.32)作为代表. 据此,估计纤度的期望.
的中点值是1.32)作为代表. 据此,估计纤度的期望. -
18.(本小题满分12分)
 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ
 .
.(Ⅰ)求证:平面VAB⊥平面VCD;
(Ⅱ)当角θ变化时,求直线BC与平面VAB所成的角的取
值范围.
-
19.(本小题满分12分)
 在平面直角坐标系xOy中,过定点C(0,p)作直线与抛物线x2=2px(p>0)相交于A、B两点.
在平面直角坐标系xOy中,过定点C(0,p)作直线与抛物线x2=2px(p>0)相交于A、B两点.(Ⅰ)若点N是点C关于坐标原点O的对称点,
求△ANB面积的最小值;
(Ⅱ)是否存在垂直于y轴的直线l,使得l被以AC为直径的圆截得弦长恒为定值?若存在,求出l的方程;若不存在,说明理由.(此题不要求在答题卡上画图)
-
20.(本小题满分13分)
已知定义在正实数集上的函数f(x)=
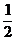 x2+2ax,g(x)=3a2lnx+b,其中a>0.设两曲线y=f(x),y=g(x)有公共点,且在该点处的切线相同.
x2+2ax,g(x)=3a2lnx+b,其中a>0.设两曲线y=f(x),y=g(x)有公共点,且在该点处的切线相同.(Ⅰ)用a表示b,并求b的最大值;
(Ⅱ)求证:f(x) ≥g(x) (x>0).
-
21.(本小题满分14分)
已知m,n为正整数.
(Ⅰ)用数学归纳法证明:当x>-1时,(1+x)m≥1+mx;
(Ⅱ)对于n≥6,已知
 ,求证
,求证 ,m=1,1,2…,n;
,m=1,1,2…,n;(Ⅲ)求出满足等式3n+4m+…+(n+2)m=(n+3)n的所有正整数n.