1．化简的结果是

　 A．2+i　　　　　 B．－2+i　　　 C．2－i　　　　　　 D．－2－i

2．

　 A．等于0　　　　 B．等于l　　　　 C．等于3　　　　　 D．不存在

3．若tan(一α)＝3，则cot α等于

A．－2　　　　　 B．－　　　　 C．　　　　　　　 D．2

4．已知(+)ⁿ展开式中，各项系数的和与其各项二项式系数的和之比为64，则n等于

　 A．4　　　　　　 B．5　　　　　　 C．6　　　　　　　 D．7

5．若0＜x＜，则下列命题中正确的是

A．sin x＜　　 B．sin x＞　　 C．sin x＜　　 D．sin x＞

6．若集合M＝{0，l，2}，N＝{(x，y)|x－2y+1≥0且x－2y－1≤0，x，y ∈M}，则N中元素的个数为

　 　A．9　　 　　　　　B．6　　 　　　　　C．4　　 　　　　　　D．2

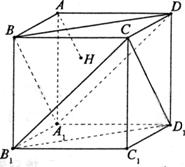
7．如图，正方体AC₁的棱长为1，过点A作平面A₁BD的垂线，

垂足为点H．则以下命题中，错误的命题是

　 　A．点H是△A₁BD的垂心

　　B．AH垂直平面CB₁D₁

　 　C．AH的延长线经过点C₁

　 　D．直线AH和BB₁所成角为45°

8．四位好朋友在一次聚会上，他们按照各自的爱好选择了形状不同、内空高度相等、杯口半径相等的圆口酒杯，如图所示．盛满酒后他们约定：先各自饮杯中酒的一半．设剩余酒的高度从左到右依次为h₁，h₂，h₃，h₄，则它们的大小关系正确的是

A．h₂＞h₁＞h₄　　 B．h₁＞h₂＞h₃　　 　C．h₃＞h₂＞h₄ 　　　D．h₂＞h₄＞h₁

9．设椭圆的离心率为e＝，右焦点为F(c，0)，方程ax²+bx－c＝0的两个实根分别为x₁和x₂，则点P(x₁，x₂)

A．必在圆x²+y²＝2内　　 　　　　　B．必在圆x²+y²＝2上

C．必在圆x²+y²＝2外　　 　　　　　D．以上三种情形都有可能

10．将一个骰子连续抛掷三次，它落地时向上的点数依次成等差数列的概率为

　 　A．　 　　　　B．　　 　　　C．　　 　　　　D．

11．设函数f(x)是R上以5为周期的可导偶函数，则曲线y＝f(x)在x＝5处的切线的斜率为

　 　A．－　　 　　B．0　　 　　　　C．　　 　　　　　D．5

12．设p：f(x)＝e^x+In x+2x²+mx+l在(0，+∞)内单调递增，q：m≥－5，则p是q的

　 　A．充分不必要条件　 　　　　　　B．必要不充分条件

　 　C．充分必要条件　　 　　　　　　D．既不充分也不必要条件

绝密启用前

理科数学

第Ⅱ卷

　　 第Ⅱ卷2页，须用黑色墨水签字笔在答题卡上书写作答．若在试题卷上作答，答案无效．

13．设函数y＝4+log₂(x－1)(x≥3)，则其反函数的定义域为　　　　　 ．

14．已知数列{a_n}对于任意p，q ∈N^*，有a_p+a_q=a_p+q，若a₁=，则a₃₆＝　　　　 ．

15．如图，在△ABC中，点O是BC的中点，过点O的直

线分别交直线AB、AC于不同的两点M、N，若＝

m，＝n，则m+n的值为　　　　　 ．

16．设有一组圆C_k：(x－k+1)²+(y－3k)²＝2k⁴ (k∈N^*)．下　

列四个命题：　

A．存在一条定直线与所有的圆均相切

B．存在一条定直线与所有的圆均相交

C．存在一条定直线与所有的圆均不相交

D．所有的圆均不经过原点

其中真命题的代号是　　 ．(写出所有真命题的代号)

17．(本小题满分12分)

　 　已知函数在区间(0，1)内连续，且．

　 　(1)求实数k和c的值；

　 　(2)解不等式

18．(本小题满分12分)

如图，函数y＝2cos(ωx+θ) (x∈R，0≤θ≤)的

图象与y轴交于点(0，)，且在该点处切线的斜

率为一2．

　 　(1)求θ和ω的值；

　 　(2)已知点A(，0)，点P是该函数图象上一点，点Q(x₀，y₀)是PA的中点，当y₀＝，x∈[，π]时，求x₀的值．

19．(本小题满分12分)

　 　某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品，制作过程必须先后经过两次烧制，当第一次烧制合格后方可进入第二次烧制，两次烧制过程相互独立．根据该厂现有的技术水平，经过第一次烧制后，甲、乙、丙三件产品合格的概率依次为0.5，　 0.6，　 0.4．经过第二次烧制后，甲、乙、丙三件产品合格的概率依次为0.6，0.5，0.75．

　 　(1)求第一次烧制后恰有一件产品合格的概率；

　 　(2)经过前后两次烧制后，合格工艺品的个数为ξ，求随机变量ξ的期望．

20．(本小题满分12分)

　 　右图是一个直三棱柱(以A₁B₁C₁为底面)被一平面所截得到

　 　的几何体，截面为ABC．已知A₁B₁＝B₁C₁＝l，∠A_lB_lC₁＝90°，

　 　AA_l＝4，BB_l＝2，CC_l＝3．

　 　(1)设点O是AB的中点，证明：OC∥平面A₁B₁C₁；

　 　(2)求二面角B-AC-A₁的大小；

　 　(3)求此几何体的体积．

21．(本小题满分12分)

　 　设动点P到点A(－l，0)和B(1，0)的距离分别为d₁和d₂，

　 　∠APB＝2θ，且存在常数λ(0＜λ＜1)，使得d₁d₂ sin²θ＝λ．

　 　(1)证明：动点P的轨迹C为双曲线，并求出C的方程；

　 (2)过点B作直线交双曲线C的右支于M、N两

　 　　　点，试确定λ的范围，使.＝0，其中点

　　 　　O为坐标原点．

22．(本小题满分14分)

　 　设正整数数列{a_n}满足：a₂＝4，且对于任何

　　 n∈N^*，有．

　 　(1)求a₁，a₃；

　 　(2)求数列{ a_n }的通项a_n ．