-
1、已知
 则
则 与
与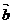 的夹角等于
的夹角等于A.90° B.30° C.60° D.150°
-
2、设M、O、A、B、C是空间的点,则使M、A、B、C一定共面的等式是
A.
 B.
B.
C.
 D.
D.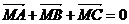
-
3、下列命题不正确的是
A.过平面外一点有且只有一条直线与该平面垂直;
B.如果平面的一条斜线在平面内的射影与某直线垂直,则这条斜线必与这条直线垂直;
C.两异面直线的公垂线有且只有一条;
D.如果两个平行平面同时与第三个平面相交,则它们的交线平行。
-
4、若
 、
、 表示直线,
表示直线, 表示平面,则下列命题中,正确的个数为
表示平面,则下列命题中,正确的个数为 ①
 ②
② ③
③ ④
④
A.1个 B.2个 C.3个 D.4个
-
5、四棱锥成为正棱锥的一个充分但不必要条件是
A.各侧面是正三角形 B.底面是正方形
C.各侧面三角形的顶角为45度 D.顶点到底面的射影在底面对角线的交点上
-
6、若点A(
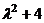 ,4-μ,1+2γ)关于y轴的对称点是B(-4λ,9,7-γ),则λ,μ,γ的值依次为
,4-μ,1+2γ)关于y轴的对称点是B(-4λ,9,7-γ),则λ,μ,γ的值依次为A.1,-4,9 B.2,-5,-8 C.-3,-5,8 D.2,5,8
-
7、已知一个简单多面体的各个顶点处都有三条棱,则顶点数V与面数F满足的关系式是
A.2F+V=4 B.2F-V=4 C.2F+V=2 (D)2F-V=2
-
8、侧棱长为2的正三棱锥,若其底面周长为9,则该正三棱锥的体积是
A.
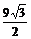 B.
B.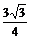 C.
C. D.
D.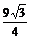
-
9、正方体ABCD-A1B1C1D1中,E、F分别是棱AB,BB1的中点,A1E与C1F所成的角是θ,则
A.θ=600 B.θ=450 C.
 D.
D.
-
10、已知球面的三个大圆所在平面两两垂直,则以三个大圆的交点为顶点的八面体的体积与球体积之比是
A.2∶π B.1∶2π C.1∶π D.4∶3π
-
11、设A,B,C,D是空间不共面的四点,且满足
 ,
,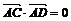 ,
,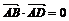 ,则△BCD是
,则△BCD是A.钝角三角形 B.直角三角形 C.锐角三角形 D.不确定
-
12、将
 =600,边长为1的菱形ABCD沿对角线AC折成二面角
=600,边长为1的菱形ABCD沿对角线AC折成二面角 ,若
,若 [60°,120°],
[60°,120°], 则折后两条对角线之间的距离的最值为
则折后两条对角线之间的距离的最值为A.最小值为
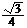 ,
最大值为
,
最大值为 B.最小值为
B.最小值为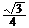 , 最大值为
, 最大值为
C.最小值为
 , 最大值为
, 最大值为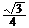 D.最小值为
D.最小值为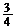 , 最大值为
, 最大值为
-
13、已知向量
 、
、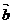 满足|
满足| | =
| =  ,|
,| | = 6,
| = 6, 与
与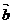 的夹角为
的夹角为 ,则3|
,则3| |-2(
|-2( .
.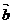 )+4|
)+4|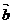 | =________;
| =________; -
14、若AB与CD是异面直线,向量

 ,
,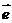 是与
是与 同向的单位向量,则
同向的单位向量,则 在
在 上的射影长是
;(用
上的射影长是
;(用 表示)
表示) -
15、如图,在四棱锥P-ABCD中,E为CD上的动点,四边形ABCD为 时,体积VP-AEB恒为定值(写上你认为正确的一个答案即可).
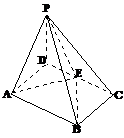
-
16、已知
 ,
,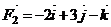 ,
, 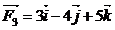 ,若
,若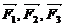 共同作用在物体上,使物体从点
共同作用在物体上,使物体从点 (2,-3,2)移到
(2,-3,2)移到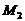 (4,2,3),则合力所作的功
;
(4,2,3),则合力所作的功
; -
17、若棱锥底面面积为
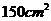 ,平行于底面的截面面积是
,平行于底面的截面面积是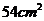 ,底面和这个截面的距离是
,底面和这个截面的距离是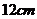 ,则棱锥的高为 ;
,则棱锥的高为 ; -
18、一个四面体的所有棱长都是
 ,四个顶点在同一个球面上,则此球的表面积为 .
,四个顶点在同一个球面上,则此球的表面积为 . -
19、设空间两个不同的单位向量
 =(x1, y1 ,0),
=(x1, y1 ,0), =(x2, y2,0)与向量
=(x2, y2,0)与向量 =(1,1,1)的夹角都等于
=(1,1,1)的夹角都等于 ,求
,求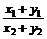 的值(6分)
的值(6分) -
20、在正方体ABCD─A1B1C1D1中,M、N、P分别是A1B1,BB1,B1C1的中点,用空间向量的坐标运算证明:B1D
 平面PMN。(6分)
平面PMN。(6分) -
21、球面上三点A、B、C组成这个球的一个截面的内接三角形,AB=18,BC=24,
AC=30,且球心到该截面的距离为球半径的一半。
(1)求球的表面积;
(2)求A,C两点的球面距离。(8分)
-
22、
 如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90º,
如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90º,棱AA1=2,M、N分别是A1B1,A1A的中点,
(I)求
 的长;
的长; (II)求cos<
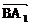 ,
,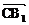 >的值;
>的值;(III)求证:A1B⊥C1M.(9分)
-
23、如图,正方形ACC1A1与等腰直角△ACB互相垂直,∠ACB=90°,E、F分别是AB、BC的中点, G是AA1上的点.
(I)若
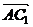

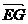 ,试确定点G的位置;
,试确定点G的位置;(II)在满足条件(1)的情况下,试求cos<
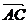 ,
, >的值.(8分)
>的值.(8分)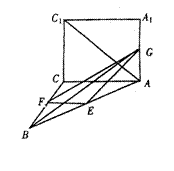
-
24、在正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,M为D1D的中点.
(I)求证:异面直线B1O与AM垂直;
(II)求二面角B1-AM-C的大小;
(III)若正方体的棱长为a,求三棱锥B1-AMC的体积。(9分)

高中数学必修内容复习(9)--- 直线、平面、简单几何体参考答案
答案
1、D 2、D 3、B 4、C 5、A 6、B 7、B 8、B 9、C 10、C 11、C 12、B
13、23
14、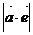 15、AB∥CD 16、16 17、30cm 18、3
15、AB∥CD 16、16 17、30cm 18、3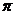
19、1
20、略;
21、1200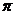 ;
;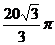 ;
;
22、 ;
; ;略;
;略;
23、中点; ;
;
24、略;arctan ;
; .
.