-
1.已知a>b>0,全集为R,集合
 ,
, ,
, ,则有
,则有A.
 (
(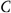
 )
B.
)
B. (
(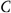
 )
)
C.
 D.
D.
-
2.已知实数a,b均不为零,
 ,且
,且 ,则
,则 等于
等于A.
 B.
B. C.
C. D.
D.
-
3.已知函数
 的图像关于点(-1,0)对称,且当
的图像关于点(-1,0)对称,且当 (0,+∞)时,
(0,+∞)时, ,则当
,则当 (-∞,-2)时
(-∞,-2)时 的解析式为
的解析式为A.
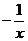 B.
B. C.
C. D.
D.
-
4.已知
 是第三象限角,
是第三象限角, ,且
,且 ,则
,则 等于
等于A.
 B.
B. C.
C. D.
D.
-
5.(理)已知抛物线
 上两个动点B、C和点A(1,2)且∠BAC=90°,则动直线BC必过定点
上两个动点B、C和点A(1,2)且∠BAC=90°,则动直线BC必过定点A.(2,5) B.(-2,5) C.(5,-2) D.(5,2)
(文)过抛物线
 的焦点作直线交抛物线于
的焦点作直线交抛物线于 ,
, 、
、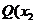 ,
, 两点,若
两点,若 ,则
,则 等于
等于A.4p B.5p C.6p D.8p
-
6.设a,b,c是空间三条直线,
 ,
, 是空间两个平面,则下列命题中,逆命题不成立的是
是空间两个平面,则下列命题中,逆命题不成立的是A.当c⊥
 时,若c⊥
时,若c⊥ ,则
,则 ∥
∥
B.当
 时,若b⊥
时,若b⊥ ,则
,则
C.当
 ,且c是a在
,且c是a在 内的射影时,若b⊥c,则a⊥b
内的射影时,若b⊥c,则a⊥bD.当
 ,且
,且 时,若c∥
时,若c∥ ,则b∥c
,则b∥c -
7.两个非零向量a,b互相垂直,给出下列各式:
①a.b=0;②a+b=a-b;③|a+b|=|a-b|;④|a|
 +|b|
+|b| =
= a+b
a+b ;⑤(a+b).(a-b)=0.
;⑤(a+b).(a-b)=0.其中正确的式子有
A.2个 B.3个 C.4个 D.5个
-
8.已知数列
 的前n项和为
的前n项和为 ,
, ,现从前m项:
,现从前m项: ,
, ,…,
,…, 中抽出一项(不是
中抽出一项(不是 ,也不是
,也不是 ),余下各项的算术平均数为37,则抽出的是
),余下各项的算术平均数为37,则抽出的是A.第6项 B.第8项 C.第12项 D.第15项
-
9.已知双曲线
 (a>0,b>0)的两个焦点为
(a>0,b>0)的两个焦点为 、
、 ,点A在双曲线第一象限的图象上,若△
,点A在双曲线第一象限的图象上,若△ 的面积为1,且
的面积为1,且 ,
, ,则双曲线方程为
,则双曲线方程为A.
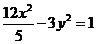 B.
B.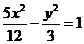
C.
 D.
D.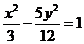
-
10.在正三棱锥A-BCD中,E,F分别是AB,BC的中点,EF⊥DE,且BC=1,则正三棱锥A-BCD的体积等于
A.
 B.
B. C.
C. D.
D.
-
11.(理)某城市新修建的一条道路上有12盏路灯,为了节省用电而又不能影响正常的照明,可以熄灭其中的3盏灯,但两端的灯不能熄灭,也不能熄灭相邻的两盏灯,则熄灯的方法有
A.
 种
B.
种
B. 种 C.
种 C. 种 D.
种 D. 种
种(文)某师范大学的2名男生和4名女生被分配到两所中学作实习教师,每所中学分配1名男生和2名女生,则不同的分配方法有
A.6种 B.8种 C.12种 D.16种
-
12.已知
 是定义在R上的偶函数,且对任意
是定义在R上的偶函数,且对任意 ,都有
,都有 ,当
,当 [4,6]时,
[4,6]时, ,则函数
,则函数 在区间[-2,0]上的反函数
在区间[-2,0]上的反函数 的值
的值 为
为A.
 B.
B. C.
C. D.
D.
第Ⅱ卷(非选择题,共90分)
-
13.(理)已知复数
 ,
, ,则复数
,则复数 的虚部等于________.
的虚部等于________.(文)从某社区150户高收入家庭,360户中等收入家庭,90户低收入家庭中,用分层抽样法选出100户调查社会购买力的某项指标,则三种家庭应分别抽取的户数依次为________.
-
14.若实数a,b均不为零,且
 ,则
,则 展开式中的常数项等于________.
展开式中的常数项等于________. -
15.代号为“狂飙”的台风于某日晚8点在距港口的A码头南偏东60°的400千米的海面上形成,预计台风中心将以40千米/时的速度向正北方向移动,离台风中心350千米的范围都会受到台风影响,则A码头从受到台风影响到影响结束,将持续多少小时________.
-
16.给出下列4个命题:
①函数
 是奇函数的充要条件是m=0:
是奇函数的充要条件是m=0:②若函数
 的定义域是
的定义域是 ,则
,则 ;
;③若
 ,则
,则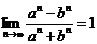 (其中
(其中 );
);④圆:
 上任意点M关于直线
上任意点M关于直线 的对称点,
的对称点,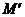 也在该圆上.
也在该圆上.填上所有正确命题的序号是________.
-
17.(12分)
已知二次函数
 对任意
对任意 ,都有
,都有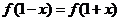 成立,设向量
成立,设向量 (sinx,2),
(sinx,2), (2sinx,
(2sinx, ),
), (cos2x,1),
(cos2x,1), (1,2),当
(1,2),当 [0,
[0, ]时,求不等式f(
]时,求不等式f( )>f(
)>f( )的解集.
)的解集. -
18.(12分)
(理)甲、乙队进行篮球总决赛,比赛规则为:七场四胜制,即甲或乙队,谁先累计获胜四场比赛时,该队就是总决赛的冠军,若在每场比赛中,甲队获胜的概率均为0.6,每场比赛必须分出胜负,且每场比赛的胜或负不影响下一场比赛的胜或负.
(1)求甲队在第五场比赛后获得冠军的概率;
(2)求甲队获得冠军的概率;
(文)有甲、乙两只口袋,甲袋装有4个白球2个黑球,乙袋装有3个白球和4个黑球,若从甲、乙两袋中各任取出两球后并交换放入袋中.
(1)求甲袋内恰好有2个白球的概率;
(2)求甲袋内恰好有4个白球的概率;
注意:考生在(19甲)、(19乙)两题中选一题作答,如果两题都答,只以(19甲)计分.
19甲.(12分)
如图,正三棱锥P-ABC,PA=4,AB=2,D为BC中点,点E在AP上,满足AE=3EP.
 (1)建立适当坐标系,写出A、B、D、E四点的坐标;
(1)建立适当坐标系,写出A、B、D、E四点的坐标;(2)求异面直线AD与BE所成的角.
 19乙.(12分)如图,长方体
19乙.(12分)如图,长方体 中,
中, ,
, ,M是AD中点,N是
,M是AD中点,N是 中点.
中点.(1)求证:
 、M、C、N四点共面;
、M、C、N四点共面;(2)求证:
 ;
;(3)求证:平面
 ⊥平面
⊥平面 ;
;(4)求
 与平面
与平面 所成的角.
所成的角. -
20.(12分)
已知函数
 .
.(1)若
 在
在 [1,+∞
[1,+∞ 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;(2)若x=3是
 的极值点,求
的极值点,求 在
在 [1,a]上的最小值和最大值.
[1,a]上的最小值和最大值. -
21.(12分)
已知椭圆方程为
 ,射线
,射线 (x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).
(x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).(1)求证直线AB的斜率为定值;
(2)求△
 面积的最大值.
面积的最大值. -
22.(14分)
已知等差数列
 的首项为a,公差为b;等比数列
的首项为a,公差为b;等比数列 的首项为b,公比为a,其中a,
的首项为b,公比为a,其中a, ,且
,且 .
.(1)求a的值;
(2)若对于任意
 ,总存在
,总存在 ,使
,使 ,求b的值;
,求b的值;(3)在(2)中,记
 是所有
是所有 中满足
中满足 ,
,  的项从小到大依次组成的数列,又记
的项从小到大依次组成的数列,又记 为
为 的前n项和,
的前n项和,
 的前n项和,求证:
的前n项和,求证: ≥
≥
 .
.
08高考数学冲刺预测卷三 说明:本套试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分.考试时间:120分钟. 第Ⅰ卷(选择题,共60分)参考答案
参考答案
1.A 2.B 3.B 4.D 5.(理)C (文)A 6.B 7.A 8.B 9.A 10.B 11.(理)A (文)C 12.B
13.(理) (文)25,60,15 14.-672 15.2.5小时 16.①,④
(文)25,60,15 14.-672 15.2.5小时 16.①,④
17.设f(x)的二次项系数为m,其图象上两点为(1-x, )、B(1+x,
)、B(1+x, )
)
因为 ,
,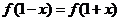 ,所以
,所以 ,
,
由x的任意性得f(x)的图象关于直线x=1对称,
若m>0,则x≥1时,f(x)是增函数,若m<0,则x≥1时,f(x)是减函数.
∵  ,
, ,
, ,
, ,
,
 ,
,
∴ 当 时,
时,




 ,
, .
.
∵  , ∴
, ∴ 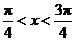 .
.
当 时,同理可得
时,同理可得 或
或 .
.
综上: 的解集是当
的解集是当 时,为
时,为 ;
;
当 时,为
时,为 ,或
,或 .
.
18.(理)(1)设甲队在第五场比赛后获得冠军为事件M,则第五场比赛甲队获胜,前四场比赛甲队获胜三场,依题意得 .
.
(2)设甲队获得冠军为事件E,则E包含第四、第五、第六、第七场获得冠军四种情况,且它们被彼此互斥.
∴  .
.
(文)设甲袋内恰好有4个白球为事件B,则B包含三种情况.
①甲袋中取2个白球,且乙袋中取2个白球,②甲袋中取1个白球,1个黑球,且乙袋中取1个白球,1个黑球,③甲、乙两袋中各取2个黑球.
∴ 
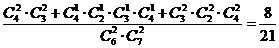 .
.
 19.(甲)(1)建立如图坐标系:O为△ABC的重心,直线OP为z轴,AD为y轴,x轴平行于CB,得A(0,
19.(甲)(1)建立如图坐标系:O为△ABC的重心,直线OP为z轴,AD为y轴,x轴平行于CB,得A(0, ,0)、B(1,
,0)、B(1, ,0)、D(0,
,0)、D(0, ,0)、E(0,
,0)、E(0,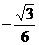 ,
, ).
).
 (2)
(2)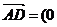 ,
, ,
, ,
, ,
, ,设AD与BE所成的角为
,设AD与BE所成的角为 ,则
,则 .∴
.∴  .
.
(乙)(1)取 中点E,连结ME、
中点E,连结ME、 ,∴
,∴ 

 ,MC
,MC EC.∴
EC.∴ 
 MC.∴
MC.∴  ,M,C,N四点共面.
,M,C,N四点共面.
(2)连结BD,则BD是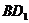 在平面ABCD内的射影.
在平面ABCD内的射影.
∵ 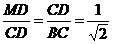 , ∴ Rt△CDM-Rt△BCD,∠DCM=∠CBD.
, ∴ Rt△CDM-Rt△BCD,∠DCM=∠CBD.
∴ ∠CBD+∠BCM=90°. ∴ MC⊥BD.∴  .
.
(3)连结 ,由
,由 是正方形,知
是正方形,知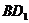 ⊥
⊥ .
.
∵ 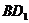 ⊥MC, ∴
⊥MC, ∴  ⊥平面
⊥平面 .
.
∴ 平面 ⊥平面
⊥平面 .
.
(4)∠ 是
是 与平面
与平面 所成的角且等于45°.
所成的角且等于45°.
20.(1) .∵ x≥1. ∴
.∵ x≥1. ∴ 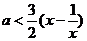 ,
,
当x≥1时, 是增函数,其最小值为
是增函数,其最小值为 .
.
∴ a<0(a=0时也符合题意). ∴ a≤0.
(2) ,即27-6a-3=0, ∴ a=4.
,即27-6a-3=0, ∴ a=4.
∴  有极大值点
有极大值点 ,极小值点
,极小值点 .
.
此时f(x)在 ,
, 上时减函数,在
上时减函数,在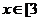 ,+
,+ 上是增函数.
上是增函数.
∴ f(x)在 ,
, 上的最小值是
上的最小值是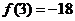 ,最大值是
,最大值是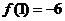 ,(因
,(因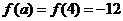 ).
).
21.(1)∵斜率k存在,不妨设k>0,求出M( ,2).直线MA方程为
,2).直线MA方程为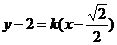 ,直线MB方程为
,直线MB方程为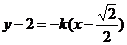 .
.
分别与椭圆方程联立,可解出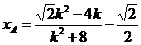 ,
, .
.
∴  . ∴
. ∴  (定值).
(定值).
(2)设直线AB方程为 ,与
,与 联立,消去y得
联立,消去y得
 .
.
由>0得-4<m<4,且m≠0,点M到AB的距离为 .
.
设△AMB的面积为S. ∴  .
.
当 时,得
时,得 .
.
22.(1)∵  ,a,
,a, ,
,
∴  ∴
∴ 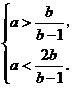 ∴
∴  ∴
∴  .
.
∴ a=2或a=3(a=3时不合题意,舍去). ∴a=2.
(2) ,
, ,由
,由 可得
可得 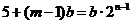 .
.
∴  .∴ b=5
.∴ b=5
(3)由(2)知 ,
, , ∴
, ∴  .
.
∴  . ∴
. ∴  ,
, .
.
∵  ,
, .
.
当n≥3时,



 .
.
∴  . 综上得
. 综上得 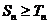
 .
.