-
1.一种专门占据内存的计算机病毒开始时占据内存2KB,工作时3分钟自身复制一次,(即复制后所占内存是原来的2倍),那么,开机后( )分钟,该病毒占据64MB(
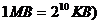 。
。 A. 45 B.
48 C. 51 D. 42
A. 45 B.
48 C. 51 D. 42 -
2.观察新生婴儿的体重,其频率分布直方图如图所示,则新生婴儿的体重在[2700,3000]的频率为( )
A. 0.001 B. 0.003
C. 0.01 D. 0.3
-
3.
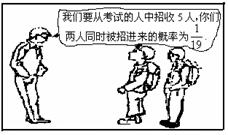 两位同学去某大学参加自主招生考试,根据右图学校负责人与他们两人的对话,可推断出参加考试的人数为
( )
两位同学去某大学参加自主招生考试,根据右图学校负责人与他们两人的对话,可推断出参加考试的人数为
( ) A. 19 B. 20
C. 21 D.22
-
4.有两排座位,前排11个座位,后排12个座位,现安排2人就座,规定前排中间的3个座位不能坐,并且这2人不左右相邻,那么不同排法的种数是 ( )
A.234 B.346 C.350 D.363
-
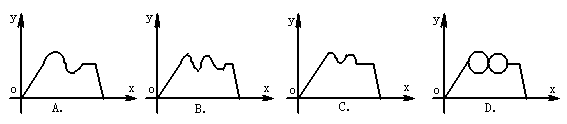
5.福州某中学的研究性学习小组为考察闽江口的一个小岛的湿地开发情况,从某码头乘汽艇出发,沿直线方向匀速开往该岛,靠近岛时,绕小岛环行两周后,把汽艇停靠岸边上岸考察,然后又乘汽艇沿原航线提速返回。设t为出发后的某一时刻,S为汽艇与码头在时刻t的距离,下列图象中能大致表示S=f(x)的函数关系的为 ( )
-
6.某金店用一杆不准确的天平(两边臂不等长)称黄金,某顾客要购买
 黄金,售货员先 将
黄金,售货员先 将 的砝码放在左盘,将黄金放于右盘使之平衡后给顾客;然后又将
的砝码放在左盘,将黄金放于右盘使之平衡后给顾客;然后又将 的砝码放入右 盘,将另一黄金放于左盘使之平衡后又给顾客,则顾客实际所得黄金
( )
的砝码放入右 盘,将另一黄金放于左盘使之平衡后又给顾客,则顾客实际所得黄金
( )A.大于
 B.小于
B.小于 C.大于等于
C.大于等于 D.小于等于
D.小于等于
-
7.13年前一笔扶贫助学资金,每年的存款利息(年利率11.34%,不纳税)可以资助100人上学,平均每人每月94.50元,现在(存款利率1.98%,并且扣20%的税)用同样一笔资金每年的存款利息最多可以资助多少人上学(平均每人每月100元) ( )
A、10 B、13 C、15 D、20
-
8.
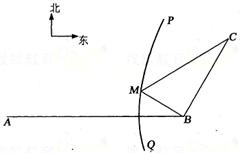 如图,B地在A地的正东方向4 km处,C地在B地的北偏东30º方向2 km处,现要在曲线PQ上任意选一处M建一座码头,向B、C两地转运货物,经测算,从M到B、C两地修建公路的费用都是a万元/km、那么修建这两条公路的总费用最低是( )
如图,B地在A地的正东方向4 km处,C地在B地的北偏东30º方向2 km处,现要在曲线PQ上任意选一处M建一座码头,向B、C两地转运货物,经测算,从M到B、C两地修建公路的费用都是a万元/km、那么修建这两条公路的总费用最低是( )A.(
 +1)a万元 B.(2
+1)a万元 B.(2 -2) a万元
-2) a万元
C.2
 a万元 D.(
a万元 D.( -1) a万元
-1) a万元 -
9.设
 是某港口水的深度y(米)关于时间t(时)的函数,其中
是某港口水的深度y(米)关于时间t(时)的函数,其中 .下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:t
0
3
6
9
12
15
18
21
24
y
12
15.1
12.1
9.1
11.9
14.9
11.9
8.9
12.1
经长期观观察,函数
 的图象可以近似地看成函数
的图象可以近似地看成函数 的图象.在下面的函数中,最能近似表示表中数据间对应关系的函数是 ( )
的图象.在下面的函数中,最能近似表示表中数据间对应关系的函数是 ( )A.
 B.
B.
C.
 D.
D.
-
10.椭圆有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆壁反射后,反射光线经过椭圆的另一个焦点.今有一个水平放置的椭圆形台球盘,点
 、
、 是它的焦点,长轴长为
是它的焦点,长轴长为 ,焦距为
,焦距为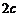 ,静放在点
,静放在点 的小球(小球的半径不计),从点
的小球(小球的半径不计),从点 沿直线出发,经椭圆壁反弹后第一次回到点
沿直线出发,经椭圆壁反弹后第一次回到点 时,小球经过的路程是
( )
时,小球经过的路程是
( )(A)
 (B)
(B) (C)
(C) (D)以上答案均有可能
(D)以上答案均有可能 -
11.某新区新建有5个住宅小区(A、B、C、D、E),现要铺设连通各小区的自来水管道,如果它们两两之间的线路长如下表:
地
地
离
距
名
名
(km)


A
B
C
D
E
A
5
7
8
5
B
3
5
2
C
5
4
D
4
E
请问:最短的管线长为 ( )
A.13 B.14 C.15 D.17
-
12.某地2004年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下
行业名称
计算机
机械
营销
物流
贸易
应聘人数
215830
200250
154676
74570
65280
行业名称
计算机
营销
机械
建筑
化工
招聘人数
124620
102935
89115
76516
70436
若用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,则根据表中数据,就业形势一定是 ( )
A.计算机行业好于化工行业. B. 建筑行业好于物流行业.
C.机械行业最紧张. D. 营销行业比贸易行业紧张.
-
13.毛泽东在《送瘟神》中写到:“坐地日行八万里”。又知地球的体积大约是火星的8倍,则火星的大圆周长约______________万里。
-
14.一个总体中有100个个体,随机编号0,1,2,…,99,依编号顺序平均分成10个小组,组号依次为1,2,3,…,10.现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k组中抽取的号码个位数字与m+k的个位数字相同,若m=6,则在第7组中抽取的号码是 .
-
15.图1,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器(图2).当这个正六棱柱容器的底面边长为 时,其容积最大.

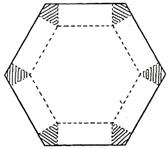
图1
-
16.代号为“狂飙”的台风于某日晚8点在距港口的A码头南偏东60°的400千米的海面上形成,预计台风中心将 以40千米/时的速度向正北方向移动,离台风中心350千米的范围都会受到台风影响,则A码头从受到台风影响到影响结束,将持续多少小时________.
-
17.某村计划建造一个室内面积为 800m2的矩形蔬菜温室.在温室内,沿左、右两侧与后侧内墙各保留 lm 宽的通道,沿前侧内墙保留3m宽的空地.当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
-
18.某工厂生产某种产品,已知该产品的月生产量
 (吨)与每吨产品的价格
(吨)与每吨产品的价格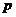 (元/吨)之间的关系式为:
(元/吨)之间的关系式为: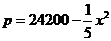 ,且生产x吨的成本为
,且生产x吨的成本为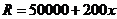 (元)。问该产每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入─成本)
(元)。问该产每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入─成本) -
19.为防止某突发事件发生,有甲、乙、丙、丁四种相互独立的预防措施可供采用,单独采用甲、乙、丙、丁预防措施后此突发事件不发生的概率(记为P)和所需费用如下表:
预防措施
甲
乙
丙
丁
P
0.9
0.8
0.7
0.6
费用(万元)
90
60
30
10
预防方案可单独采用一种预防措施或联合采用几种预防措施,在总费用不超过120万元的前提下,请确定一个预防方案,使得此突发事件不发生的概率最大.
-
20.某人上午7时,乘摩托艇以匀速v海里/时(4≤v≤20)从A港出发到距50海里的B港去,然后乘汽车以w千米/时(30≤w≤100)自B港向距300千米的C市驶去,应该在同一天下午4至9点到达C市.设汽车、摩托艇所需的时间分别是x、y小时.
(1)作图表示满足上述条件x、y的范围;
(2)如果已知所需的经费p=100+3(5-x)+2(8-y)(元),那么v、w分别是多少时走得最经济?此时需花费多少元?
-
21.某企业2003年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降.若不能进行技术改造,预测从今年起每年比上一年纯利润减少20万元,今年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第n年(今年为第一年)的利润为500(1+
 )万元(n为正整数).
)万元(n为正整数).(Ⅰ)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为An万元,进行技术改造后的累计纯利润为Bn万元(须扣除技术改造资金),求An、Bn的表达式;
(Ⅱ)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
-
22.某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到了一声巨响,正东观测点听到的时间比其他两观测点晚4s. 已知各观测点到该中心的距离都是1020m. 试确定该巨响发生的位置.(假定当时声音传播的速度为340m/ s :相关各点均在同一平面上)
高三数学应用题专题复习参考答案
参考答案
 1 A 2D
3B 4 B. 5C 6 A 7 B
8 B 9 A 10 D 11 B
12B
1 A 2D
3B 4 B. 5C 6 A 7 B
8 B 9 A 10 D 11 B
12B
13.4 14.63 15. 16 . 2.5小时
17. 解:设温室的长为xm,则宽为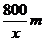 ,由已知得蔬菜的种植面积S为:
,由已知得蔬菜的种植面积S为:

 (当且仅当
(当且仅当 即x=20时,取“=”).
即x=20时,取“=”).
故:当温室的长为20m, 宽为40m时,蔬菜的种植面积最大,最大面积为648m2.
18.解:每月生产x吨时的利润为

 ,故它就是最大值点,且最大值为:
,故它就是最大值点,且最大值为:
答:每月生产200吨产品时利润达到最大,最大利润为315万元.
19. 解:方案1:单独采用一种预防措施的费用均不超过120万元.由表可知,采用甲措施,可使此突发事件不发生的概率最大,其概率为0.9.
方案2:联合采用两种预防措施,费用不超过120万元,由表可知.联合甲、丙两种预防措施可使此突发事件不发生的概率最大,其概率为
1-(1-0.9)(1-0.7)=0.97.
方法3:联合采用三种预防措施,费用不超过120万元,故只能联合乙、丙、丁三种预防措施,此时突发事件不发生的概率为
1-(1-0.8)(1-0.7)(1-0.6)=1-0.024=0.976.
综合上述三种预防方案可知,在总费用不超过120万元的前提下,联合使用乙、丙、丁三种预防措施可使此突发事件不发生的概率最大.
20. 解:(1) 由题意得:v= ,w=
,w= ,4≤v≤20,30≤w≤100,
,4≤v≤20,30≤w≤100,

∴3≤x≤10, ≤y≤
≤y≤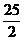 .①
.①
由于汽车、摩托艇所要的时间和x+y应在9至14小时之间,即9≤x+y≤14,②
因此满足①②的点(x,y)的存在范围是图中阴影部分(包括边界).
(2) 因为p=100+3(5-x)+2(8-y),所以3x+2y=131-p,设131-p=k,那么当k最大时,p最小,在图中通过阴影部分区域且斜率为-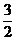 的直线3x+2y=k中,使k值最大的直线必通过点(10,4),即当y=4时,p最小,此时x=10,v=12.5,w=30,p的最小值为93元.
的直线3x+2y=k中,使k值最大的直线必通过点(10,4),即当y=4时,p最小,此时x=10,v=12.5,w=30,p的最小值为93元.
21. 解:(Ⅰ)依题设,An=(500-20)+(500-40)+…+(500-20n)=490n-10n2;
Bn=500[(1+ )+(1+
)+(1+ )+…+(1+
)+…+(1+ )]-600=500n-
)]-600=500n-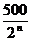 -100.
-100.
(Ⅱ)Bn-An=(500n-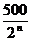 -100) -(490n-10n2)
-100) -(490n-10n2)
=10n2+10n-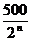 -100=10[n(n+1)
-
-100=10[n(n+1)
-  -10].
-10].
因为函数y=x(x+1) -  -10在(0,+∞)上为增函数,
-10在(0,+∞)上为增函数,
当1≤n≤3时,n(n+1) -  -10≤12-
-10≤12- -10<0;
-10<0;
当n≥4时,n(n+1) -
 -10≥20-
-10≥20- -10>0.
-10>0.
∴仅当n≥4时,Bn>An.
答:至少经过4年,该企业进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润.
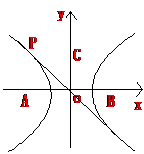 22. 解:如图,以接报中心为原点O,正东、正北方向为x轴、y轴正向,建立直角坐标系.设A、B、C分别是西、东、北观测点,则A(-1020,0),B(1020,0),C(0,1020)
22. 解:如图,以接报中心为原点O,正东、正北方向为x轴、y轴正向,建立直角坐标系.设A、B、C分别是西、东、北观测点,则A(-1020,0),B(1020,0),C(0,1020)
设P(x,y)为巨响为生点,由A、C同时听到巨响声,得|PA|=|PB|,故P在AC的垂直平分线PO上,PO的方程为y=-x,因B点比A点晚4s听到爆炸声,故|PB|- |PA|=340×4=1360
由双曲线定义知P点在以A、B为焦点的双曲线 上,
上,
依题意得a=680, c=1020,

用y=-x代入上式,得 ,∵|PB|>|PA|,
,∵|PB|>|PA|,

答:巨响发生在接报中心的西偏北450距中心 处.
处.