-
1.(05江苏卷)函数
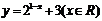 的反函数的解析表达式为(
)
的反函数的解析表达式为(
)(A)
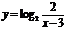 (B)
(B) (C)
(C)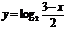 (D)
(D)
-
2. (05全国卷Ⅰ)设
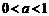 ,函数
,函数 ,则使
,则使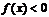 的
的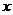 的取值范围是( )
的取值范围是( )(A)
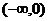 (B)
(B) (C)
(C)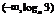 (D)
(D)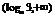
-
3. (05 全国卷III)若
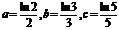 ,则( )
,则( )(A)a<b<c (B)c<b<a (C)c<a<b (D)b<a<c
-
4. (07福建卷)函数
 的图象如图,其中a、b为常数,则下列结论正确的是( )
的图象如图,其中a、b为常数,则下列结论正确的是( )A.
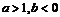 B.
B.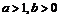 C.
C.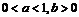 D.
D.
-
5.
 (05湖北卷)函数
(05湖北卷)函数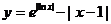 的图象大致是 ( )
的图象大致是 ( ) 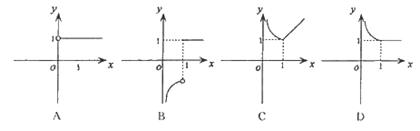
-
6.(05江西卷)函数
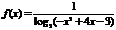 的定义域为 ( )
的定义域为 ( )A.(1,2)∪(2,3) B.
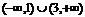 C.(1,3)
D.[1,3]
C.(1,3)
D.[1,3] -
7.(06广东卷)函数
 的定义域是
的定义域是
A.
 B.
B.  C.
C.
 D.
D. 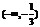
-
8.(06湖北卷)设
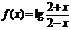 ,则
,则 的定义域为
的定义域为 A.
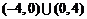 B.
B.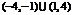
C.
 D.
D.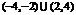
-
9.(06湖南卷)函数
 的定义域是(
)
的定义域是(
)A.(3,+∞) B.[3, +∞)C.(4, +∞) D.[4, +∞)
-
10. (06陕西卷)设函数f(x)=loga(x+b)(a>0,a≠1)的图象过点(2,1),其反函数的图像过点(2,8),则a+b等于( )
A.6 B.5 C.4 D.3
-
11. 34.(天津卷)设
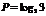 ,
,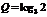 ,
,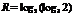 ,则( )
,则( )A.
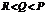 B.
B.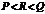 C.
C.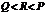 D.
D.
-
12.(浙江卷))已知
 ,则
,则 (A)1<n<m (B) 1<m<n (C)m<n<1 (D) n<m<1
-
例1.(07天津卷)已知函数
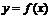 的图象与函数
的图象与函数 (
(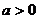 且
且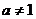 )的图象关于直线
)的图象关于直线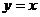 对称,记
对称,记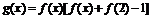 .若
.若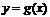 在区间
在区间 上是增函数,则实数
上是增函数,则实数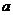 的取值范围是( )
的取值范围是( )
A.
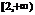 B.
B.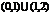 C.
C.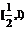 D.
D.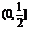
例2.(06天津卷)如果函数
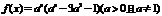 在区间
在区间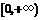 上是增函数,那么实数
上是增函数,那么实数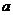 的取值范围是() A.
的取值范围是() A.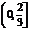 B.
B. C.
C. D.
D.
例3.(06上海卷)方程
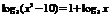 的解是_____.5
的解是_____.5例4.(07重庆卷)设
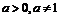 ,函数
,函数 有最小值,则不等式
有最小值,则不等式 的解集为
。x>2
的解集为
。x>2例5. (06重庆卷)已知定义域为R的函数
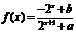 是奇函数。(Ⅰ)求
是奇函数。(Ⅰ)求 的值; (Ⅱ)若对任意的
的值; (Ⅱ)若对任意的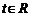 ,不等式
,不等式 恒成立,求k的取值范围;
恒成立,求k的取值范围;解析:(Ⅰ)因为f(x)是奇函数,所以f(0)=0,即
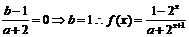
又由f(1)= -f(-1)知
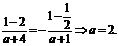
(Ⅱ)解法一:由(Ⅰ)知
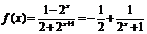 ,
,易知f(x)在
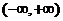 上为减函数。又因f(x)是奇函数,从而不等式:
上为减函数。又因f(x)是奇函数,从而不等式: 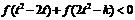 等价于
等价于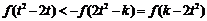 ,
,因
 为减函数,由上式推得:
为减函数,由上式推得: .即对一切
.即对一切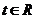 有:
有: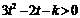 ,
,从而判别式
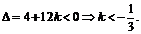
解法二:由(Ⅰ)知
 .又由题设条件得:
.又由题设条件得: 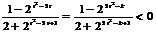 ,
,即 :
 ,
,整理得

 上式对一切
上式对一切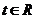 均成立,
均成立,从而判别式
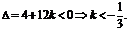
例6.证明不等式:
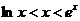
例7.定义在R上的单调函数f(x)满足f(3)=log
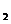 3且对任意x,y∈R都有f(x+y)=f(x)+f(y).(1)求证f(x)为奇函数;
3且对任意x,y∈R都有f(x+y)=f(x)+f(y).(1)求证f(x)为奇函数;(2)若f(k.3
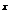 )+f(3
)+f(3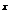 -9
-9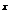 -2)<0对任意x∈R恒成立,求实数k的取值范围.
-2)<0对任意x∈R恒成立,求实数k的取值范围.解: (1)证明:f(x+y)=f(x)+f(y)(x,y∈R), ①
令x=y=0,代入①式,得f(0+0)=f(0)+f(0),即 f(0)=0.
令y=-x,代入①式,得 f(x-x)=f(x)+f(-x),又f(0)=0,
则有0=f(x)+f(-x).即f(-x)=-f(x)对任意x∈R成立,
所以f(x)是奇函数.
(2)解:f(3)=log
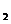 3>0,即f(3)>f(0),又f(x)在R上是单调函数,所以f(x)在R上是增函数,
3>0,即f(3)>f(0),又f(x)在R上是单调函数,所以f(x)在R上是增函数,又由(1)f(x)是奇函数.f(k.3
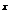 )<-f(3
)<-f(3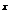 -9
-9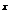 -2)=f(-3
-2)=f(-3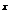 +9
+9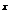 +2),
+2), ∴ k.3
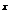 <-3
<-3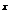 +9
+9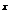 +2,3
+2,3 -(1+k).3
-(1+k).3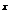 +2>0对任意x∈R成立.
+2>0对任意x∈R成立.令t=3
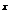 >0,问题等价于t
>0,问题等价于t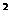 -(1+k)t+2>0
-(1+k)t+2>0对任意t>0恒成立.
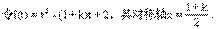



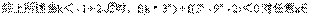 R恒成立.
R恒成立.例8.在xOy平面上有一点列P1(a1,b1),P2(a2,b2),…,Pn(an,bn)…,对每个自然数n点Pn位于函数y=2000(
 )x(0<a<1)的图象上,且点Pn,点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形
)x(0<a<1)的图象上,且点Pn,点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形 (1)求点Pn的纵坐标bn的表达式;(2)若对于每个自然数n,以bn,bn+1,bn+2为边长能构成一个三角形,求a的取值范围;(3)设Cn=lg(bn)(n∈N*),若a取(2)中确定的范围内的最小整数,问数列{Cn}前多少项的和最大?试说明理由
(1)求点Pn的纵坐标bn的表达式;(2)若对于每个自然数n,以bn,bn+1,bn+2为边长能构成一个三角形,求a的取值范围;(3)设Cn=lg(bn)(n∈N*),若a取(2)中确定的范围内的最小整数,问数列{Cn}前多少项的和最大?试说明理由
解
 (1)由题意知
(1)由题意知 an=n+
an=n+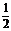 ,∴bn=2000(
,∴bn=2000( )
)

(2)∵函数y=2000(
 )x(0<a<10)递减,∴对每个自然数n,有bn>bn+1>bn+2
)x(0<a<10)递减,∴对每个自然数n,有bn>bn+1>bn+2
则以bn,bn+1,bn+2为边长能构成一个三角形的充要条件是bn+2+bn+1>bn, 即(
 )2+(
)2+( )-1>0,
)-1>0,解得a<-5(1+
 )或a>5(
)或a>5(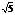 -1)
-1) ∴5(
∴5(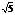 -1)<a<10
-1)<a<10
(3)∵5(
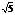 -1)<a<10,∴a=7∴bn=2000(
-1)<a<10,∴a=7∴bn=2000( )
)
 数列{bn}是一个递减的正数数列,
数列{bn}是一个递减的正数数列,对每个自然数n≥2,Bn=bnBn-1
 于是当bn≥1时,Bn<Bn-1,当bn<1时,Bn≤Bn-1,
于是当bn≥1时,Bn<Bn-1,当bn<1时,Bn≤Bn-1,因此数列{Bn}的最大项的项数n满足不等式bn≥1且bn+1<1,
由bn=2000(
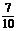 )
) ≥1得
≥1得 n≤20
n≤20 8
8 ∴n=20
∴n=20
例9.已知
 ,设P:函数
,设P:函数 在x∈(0,+∞)上单调递减;Q:曲线
在x∈(0,+∞)上单调递减;Q:曲线 与x轴交于不同两点,如果P和Q有且仅有一个正确,求
与x轴交于不同两点,如果P和Q有且仅有一个正确,求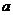 的取值范围。
的取值范围。例10.(06福建卷)已知函数f(x)=-x
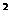 +8x,g(x)=6lnx+m
+8x,g(x)=6lnx+m(Ⅰ)求f(x)在区间[t,t+1]上的最大值h(t);
(Ⅱ)是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点?若存在,求出m的取值范围;,若不存在,说明理由。
本小题主要考查函数的单调性、极值等基本知识,考查运用导数研究函数的性质的方法,考查函数与方程、数形结合等数学思想方法和分析问题、解决问题的能力。满分12分。
本小题主要考查函数的单调性、极值、最值等基本知识,考查运用导数研究函数性质
的方法,考查运算能力,考查函数与方程、数形结合、分类与整合等数学思想方法和分析问题、解决问题的能力。
解:(I)

当t+1<4即t<3时,f(x)在[t,t+1]上单调递增,

当
 即
即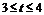 时,
时,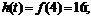
当t>4时,f(x)在[t,t+1]上单调递减,
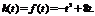 综上,
综上,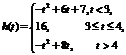
(II)函数y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点,即函数
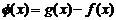 的图象与
的图象与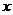 轴的正半轴有且只有三个不同的交点。
轴的正半轴有且只有三个不同的交点。
当
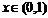 时,
时, 是增函数;
是增函数;当
 时,
时, 是减函数;
是减函数;当
 时,
时, 是增函数;
是增函数;当x=1或x=3时,
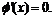

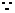 当x充分接近0时,
当x充分接近0时,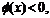 当x充分大时,
当x充分大时,
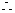 要使
要使 的图象与
的图象与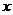 轴正半轴有三个不同的交点,必须且只须
轴正半轴有三个不同的交点,必须且只须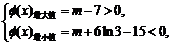
即
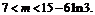 所以存在实数m,使得函数y=f(x)与y=g(x)的图象有且只有三个不同的交点,m的取值范围为(7,15-6ln3)
所以存在实数m,使得函数y=f(x)与y=g(x)的图象有且只有三个不同的交点,m的取值范围为(7,15-6ln3)