-
1、已知动点
 满足x2+y2-
满足x2+y2-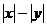 =0,
=0,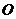 为坐标原点,则
为坐标原点,则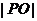 的取值范围是_______
的取值范围是_______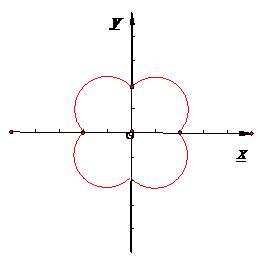 解:方程x2+y2-
解:方程x2+y2-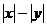 =0可化为:
=0可化为: =
=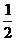
所以动点
 的轨迹如图:为原点和四段圆弧
的轨迹如图:为原点和四段圆弧故
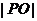 的取值范围是{0}
的取值范围是{0}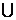

-
2、若对一切
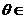 R,向量
R,向量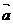 =(a+cos
=(a+cos ,2a-sin
,2a-sin )的长度不超过2,则实数
)的长度不超过2,则实数 的取值范围为
的取值范围为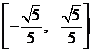 .
.解:依题意,得
 <2
<2

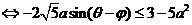 (
( )(对任意实数
)(对任意实数 成立)
成立)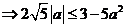
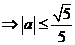 . 故
. 故  的取值范围为
的取值范围为 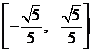 。
。 -
3、设x,y均为正实数,且
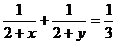 ,则xy的最小值为( )
,则xy的最小值为( )A.4 B.16 C.8 D.24
解:由
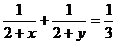 可化为xy
=8+x+y
可化为xy
=8+x+y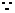 x,y均为正实数
x,y均为正实数 xy
=8+x+y
xy
=8+x+y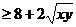 (当且仅当x=y等号成立)
(当且仅当x=y等号成立)即xy-2
 -8
-8
可解得


即xy
 16故xy的最小值为16。故选B。
16故xy的最小值为16。故选B。 -
4、设
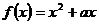 ,
, ,
,则满足条件的所有实数a的取值范围为( )
A.0<a<4 B.a=0 C.
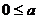 <4
D.0<a
<4
D.0<a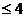
解:
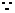
 的根为x=0或x=-a
的根为x=0或x=-a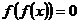 可化为
可化为 或
或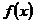 +a=0
+a=0由题意可得
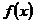 +a=0无解或
+a=0无解或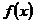 +a=0的根为x=0或x=-a
+a=0的根为x=0或x=-a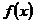 +a=0 即x2+ax+a=0
+a=0 即x2+ax+a=0
 =a2-4a<0或a=0
=a2-4a<0或a=0
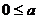 <4。故选C。
<4。故选C。 -
5、抛物线的顶点在原点,焦点在x轴的正半轴上,直线x+y-1=0与抛物线相交于A、B两点,且|AB|=
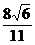 .
.(1)求抛物线的方程;
(2)在x轴上是否存在一点C,使△ABC为正三角形?若存在,求出C点的坐标:若不存在,请说明理由。
解:(1)设所求抛物线方程为
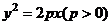 ,
,则由
 消支y得 x2-2(1+p)x+1=0
消支y得 x2-2(1+p)x+1=0设A(x1,y1)、B(x2,y2)
则x1+ x2=2(1+p) x1x2=1
由弦长|AB|=
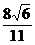 建立关于p的方程.
建立关于p的方程.解得 p=
 或p=-
或p=- (舍去)
(舍去)故抛物线方程为
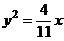 .
. (2)设AB的中点为D则D(
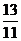 ,-
,- ),x轴上存在满足条件的点C(x0,0),
),x轴上存在满足条件的点C(x0,0),由于△ABC为正三角形.所以CD⊥AB,|CD|=
 |AB|=
|AB|=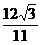 .
.由CD⊥AB得x0=
 但|CD|=
但|CD|=
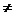
 |AB|=
|AB|=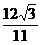
故x轴上不存在点C,使△ABC为正三角形。
-
6、已知函数
 的图像经过点
的图像经过点 和点
和点 ,且数列
,且数列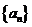 满足
满足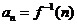 ,记数列
,记数列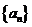 的前
的前 项和为
项和为 (
( ).
).(1)求数列
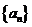 的通项公式;
的通项公式;(2)设
 ,且数列
,且数列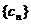 为递增数列,即对
为递增数列,即对 ,恒有
,恒有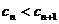 成立,试求
成立,试求 的取值范围;
的取值范围;解:(1)由条件,得

于是,
 ,
, 则
 ,
, .
.又因为
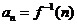 ,所以数列
,所以数列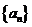 的通项公式为
的通项公式为 ,
, .
. (2)因为
 ,所以
,所以
即
 .
.
于是,
 ,因为
,因为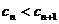 ,所以
,所以 ,
,因
 ,则
,则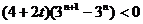
所以
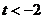 .
.