-
1.函数f (x)满足f (x+3)=x,若f-1(x)的定义域为[1,4],则f (x)的定义域为( )
A.[1,4] B.[2,8] C.[4,7] D.[3,7]
 联想:(1)函数f (x)=ax(a>0且a≠1),f-1(2)<0,则f-1(x+1)的图象是(
)
联想:(1)函数f (x)=ax(a>0且a≠1),f-1(2)<0,则f-1(x+1)的图象是(
)(2)函数y=
 (x≤-1)的反函数是
。
(x≤-1)的反函数是
。(3)函数f (x)与g (x)的图象关于直线y=x对称,函数h (x)的反函数是g (x-2),若f (3)=7,则h (3)=
。
(4)若函数y=x2-4tx+5在x∈(1,+∞)上存在反函数,则t的取值范围是 。
(5)点(2,2)既在函数f (x)=
 的图象上,又在其反函数的图象上,则适合条件的数组(a,b)有(
)
的图象上,又在其反函数的图象上,则适合条件的数组(a,b)有(
)A.1组 B.2组 C.3组 D.无数组
(6)若函数f (x)=
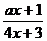 的反函数是f-1(x)=
的反函数是f-1(x)= ,则a=(
)
,则a=(
)A.1 B.-2 C.2 D.1或-2
-
2.已知a>0且a≠1,f (x)=x2-ax,当x∈(-1,1)时,均有f (x)<
 ,则实数a的取值范围是( )
,则实数a的取值范围是( )A.
 B.
B.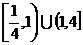 C.
C.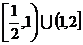 D.
D.
联想:(1)设函数f (x)=x
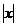 +bx+c,给出四个命题:①c=0时,y=f (x)是奇函数;②b=0,c>0时,方程f (x)=0只有一个实数根;③y=f (x)的图象关于点(o,c)对称;④方程f (x)=0至多有两个实根。上述命题中所有正确的命题的序号是
。
+bx+c,给出四个命题:①c=0时,y=f (x)是奇函数;②b=0,c>0时,方程f (x)=0只有一个实数根;③y=f (x)的图象关于点(o,c)对称;④方程f (x)=0至多有两个实根。上述命题中所有正确的命题的序号是
。(2)若不等式(关于x)
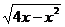 >2ax的解集为(0,2),则实数a的取值范围是
。
>2ax的解集为(0,2),则实数a的取值范围是
。(3)函数f (x)=logax在x∈
 时,
时, >1恒成立,则实数a的取值范围为( )
>1恒成立,则实数a的取值范围为( )A.
 <a<2且a≠1 B.1<a<2 C.0<a<1或1<a<2 D.a>2或0<a<
<a<2且a≠1 B.1<a<2 C.0<a<1或1<a<2 D.a>2或0<a<
(4)方程sinx+
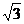 cosx=a在
cosx=a在 上有两个相异实根α,β,则实数a的取值范围是
,tan(α+β)= 。
上有两个相异实根α,β,则实数a的取值范围是
,tan(α+β)= 。 -
3.已知sinα=-
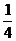 ,α∈
,α∈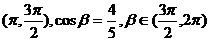 ,则α+β是( )
,则α+β是( )A.第一象限 B.第二象限 C.第三象限 D.第四象限
联想:(1)若2sin2α+sin2β-2sinα=0,则cos2α+cos2β的取值范围是( )
A.[1,5] B.[1,2] C.[1,
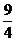 ]
D.[-1,2]
]
D.[-1,2](2)若f (x)=sin(x+
 ),x∈
),x∈ ,且关于x的方程f (x)=m有两个不等实根x1,x2,则x1+x2为( )
,且关于x的方程f (x)=m有两个不等实根x1,x2,则x1+x2为( )A.
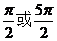 B.
B. C.
C.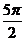 D.不确定
D.不确定(3)计算
 =
。
=
。(4)已知tanα=2,tan(α-β)=-
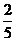 ,那么tanβ=
。
,那么tanβ=
。 -
4.已知△ABC中,
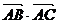 ≤0,sinA+cosA≥1,则∠A为( )
≤0,sinA+cosA≥1,则∠A为( )A.=90° B.≠90° C.>90° D.<90°
联想:(1)若
 ( )
( )A.30° B.60° C.120° D.150°
(2)已知点A(2,1),B(1,2),且
 ,则点P(x,y)的轨迹方程是 。
,则点P(x,y)的轨迹方程是 。(3)已知向量
 关于y轴对称,且
关于y轴对称,且 =1,则点P(x,y)的轨迹方程是 。
=1,则点P(x,y)的轨迹方程是 。(4)在△ABC中,
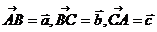 ,且
,且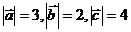 ,则
,则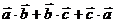 的值为
。
的值为
。(5)已知向量
 两两所成的角相等,且不共线,
两两所成的角相等,且不共线,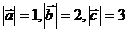 ,则向量
,则向量 的长度为
,向量
的长度为
,向量 的夹角为 。
的夹角为 。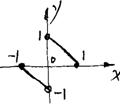 (6)若
(6)若 的夹角为120°,则
的夹角为120°,则 =
。
=
。 -
5.若不等式
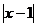 <a成立的充分条件是0<x<4,则a的取值范围是( )
<a成立的充分条件是0<x<4,则a的取值范围是( )A.a≥1 B.a≥3 C.a≤1 D.a≤3
联想:(1)若关于x的不等式
 在R上恒成立,则实数a的取值范围是( )
在R上恒成立,则实数a的取值范围是( )A.a≥1 B.a≤1 C.a≥-1 D.a≤0
(2)f (x)的图象是如图两条线段,它的定义域是
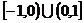 ,
,则不等式f (x)-f (-x)>-1的解集是 。
(3)若对实数
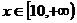 恒有
恒有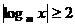 ,则实数m的取值范围是 。
,则实数m的取值范围是 。 -
6.等比数列{an}公比为q,则“a1>0,且q>1”是“对于任意自然数n,都有an+1>an”的( )
A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既非充分又非必要条件
联想(1)数列满足条件:①任意连续二项的和大于零;②任意连续三项的和小于零;则这样的数列最多有 项。
(2)a、b为不相等的正实数,且a,x,y,b成A.P,a,m,n,b成G.P,则下列关系成立是( )
A.x+y>m+n B.x+y=m+n C.x+y<m+n D.x+y与m+n的大小关系不定
(3)数列{an}是公差不为零的等差数列,并且a5,a8,a13是等比数列{bn}的相邻三项。若b2=5,则b2等于( )
A.5.
 B.5.
B.5. C.3.
C.3. D.3.
D.3.
-
7.某公司生产一种产品,固定成本为2000元,每生产一单位产品,成本增加100元,已知总收入R
 -
- +400x, 0≤x≤390
+400x, 0≤x≤390与年产量x的关系是R(x)= 则总利润最大时,每年生产的产品单
90090, x>390
位数是( )
A.150 B.200 C.250 D.300
联想:(1)设函数y=f (x)是一次函数,若f (1)=-1,且f′(-2)=-4,则f (x)为( )
A.y=-4x+3 B.y=4x-3 C.y=-4x D.y=-x
(2)如果函数y=x4-8x2+c在[-1,3]上的最小值是-14,那么c=( )
A.1 B.2 C.-1 D.-2
(3)设函数f (x)=x3+ax2+bx+c,且f (0)=0,若f (0)是函数的极值,则( )
A.b≠0 B.当a>0时,f (0)为极大值 C.b=0 D.当a<0时,f (0)为极小值
(4)已知函数f (x)=-
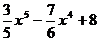 ,则
,则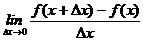 =
。
=
。(5)设函数f (x)=x3+ax2+bx-1,若当x=1时,有极值为1,则函数g(x)=x3+ax2+bx的单调递减区间为 。
-
8.四个编号分别为1、2、3、4的小球,放入编号分别为1、2、3、4的四个盒子中,每个盒子只放一个球,则有且只有一个小球和盒子的编号相同的概率是( )
A.
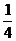 B.
B.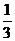 C.
C. D.
D.
联想:(1)一个口袋中有12个红球,x个白球,每次任取一球,若第10次才取到红球,其概率是
 ,则x等于( )
,则x等于( )A.8 B.7 C.6 D.5
(2)把体育组9个相同的足球放入编号为1,2,3的三个箱子里,要求每个箱子放球的个数不少于其编号数,则不同的放法共有 种。
(3)甲、乙、丙三个单位分别需要招聘工作人员2名、1名、1名,现从10名应聘人员中招聘4个甲、乙、丙三个单位,那么不同的招聘方式共有( )
A.1260种 B.2025种 C.2520种 D.5040种
-
9.若(x+1)2n展开式中,x的奇次项系数和与(x+1)n展开式中各项系数和的差为480,则(x+1)2n展开式中的第4项是( )
A.120x2 B.210x4 C.120x7 D.210x6
联想:(1)设(1+x)2+(1+2x)2+(1+3x)2+…+(1+nx)2=a0+a1x+a2x2,则
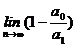 =
。
=
。(2)已知n
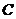
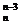 +A
+A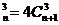 ,则
,则 展开式中不含x的项为 。
展开式中不含x的项为 。 -
10.设直线
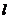 和平面α、β,且
和平面α、β,且 ,
, ,给出下列论断:①
,给出下列论断:①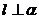 ,②α⊥β,③
,②α⊥β,③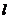 ∥β,从中取两个作为条件,其余的一个为结论,在构成的诸命题中,正确命题的个数是( )
∥β,从中取两个作为条件,其余的一个为结论,在构成的诸命题中,正确命题的个数是( )A.0 B.1 C.2 D.3
联想:已知α-a-β是大小确定的一个二面角,b和c是空间中的两条直线,下列给出的四个命题条件中,使b和c所成的角为定值的是( )
A.b∥α且c∥β B.b∥α且c⊥β C.b⊥α且c∥β D.b⊥α且c⊥β
-
11.设F1、F2是椭圆
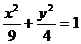 的两个焦点,P为椭圆上的一点。已知P、F1、F2是一个直角三角形的三个顶点,且
的两个焦点,P为椭圆上的一点。已知P、F1、F2是一个直角三角形的三个顶点,且 的值为
。
的值为
。联想:(1)将抛物线y2=4x绕其焦点按逆时针方向旋转90°后,所得抛物线方程为 。
(2)已知抛物线y2=2px(p>0)的焦点在直线y=x-2上,现将抛物线平移,当抛物线的焦点沿直线y=x-2移到点(2a,4a+2)时,所得抛物线的方程为 。
-
12.已知椭圆
 (a>b>0)的一个顶点的坐标为A(0,-1),且右焦点F到直线x-y+2
(a>b>0)的一个顶点的坐标为A(0,-1),且右焦点F到直线x-y+2 =0的距离为3。(1)已知椭圆的方程(2)是否存在斜率不为0的直线
=0的距离为3。(1)已知椭圆的方程(2)是否存在斜率不为0的直线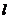 ,使其与已知椭圆交于M、N两点,满足AM⊥AN,且
,使其与已知椭圆交于M、N两点,满足AM⊥AN,且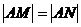 。
。联想与激活(6)
-
1.设x为直线的倾斜角,且cosx=a,-1<a<o,则x的值为( )
A.
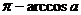 B.arccos a C. -arccos a D.
B.arccos a C. -arccos a D. 
联想:(1)直线y=
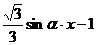 的倾斜角的变化范围是 。
的倾斜角的变化范围是 。(2)一个直角三角形三内角的正弦值成等比数列,其最小内角是( )
A.arccos
 B.arcsin
B.arcsin C.arccos
C.arccos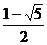 D.arcsin
D.arcsin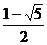
(3) 已知直线
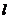 的参数方程为
的参数方程为 (t为参数),则
(t为参数),则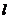 倾斜角为(
)
倾斜角为(
)A.20° B.160° C.70° D.110°
-
2.若
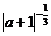 <
<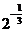 ,则a的取值范围是( )
,则a的取值范围是( )A.(-3,1) B.(-
 )∪ (1,+
)∪ (1,+ )
C.(
)
C.(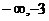 )
D.(
)
D.(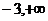 )
)联想:(1)设f(x)=2x, g(x)=4x, 且g[g(x)]>g[f(x)]>f[g(x)],则x的取值范围是( )
A.(1+∞) B.(-∞,1) C.(0,1) D.(-∞,0)
(2) 不等式
 的解集为(
)(其中a>0且a≠1)
的解集为(
)(其中a>0且a≠1)(3)设a>0, a≠1,解关于x的不等式
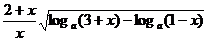 <0
<0 -
3.若函数y=
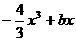 有三个单调区间,则b的取值范围是( )
有三个单调区间,则b的取值范围是( )A.b>0 B.b≥0 C.b<0 D.b≤0
联想:(1)曲线y=2x4上的点到直线y=-x-1的距离的最小值为( )
A.
 B.
B. C.
C. 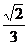 D.
D.
(2)函数y=
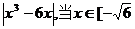 ,
, ]时,y的最大值为( )
]时,y的最大值为( )A.4
 B.3
B.3 C.2
C.2 D.
D.
(3)已知函数f(x)=x4-4x3+10x2-27,则方程f(x)=0在[2,10]上的根为( )
A.有3个 B.有2个 C.有且只有一个 D.不存在
(4)设函数f(x)=x3-
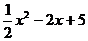 ,若对任意x
,若对任意x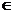 [-1,2], 都有f (x)<m,则实数m的取值范围为
。
[-1,2], 都有f (x)<m,则实数m的取值范围为
。 -
4.已知函数f(x)=2x-1,g(x)=1-x2,构造函数F(x),定义如下:
当
 ≥g(x)时,F(x)=
≥g(x)时,F(x)=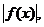 当
当 <g(x)时F(x)=-g(x),那么F(x) (
)
<g(x)时F(x)=-g(x),那么F(x) (
)A.有最小值0,无最大值 B.有最小值-1,无最大值
C.无最小值,有最大值1 D.无最小值,也无最大值
联想:(1)设函数f(x)=
 ,则f(log23)=(
)
,则f(log23)=(
)A.
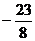 B.
B.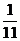 C.
C. D.
D.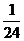
(2)若函数f(x)具有性质:①f(x)为偶函数; ②对任意x∈R,都有f(
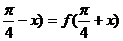 ,则函数f(x)的解析式可以是 .(只须写出满足条件的f(x)的一个解析式即可)
,则函数f(x)的解析式可以是 .(只须写出满足条件的f(x)的一个解析式即可)(3)设函数f(x)=x2-x+a (a>0),若f(m)<0,则f(m-1)与0的大小关系是 。
-
5.设A,B,C是△ABC的三个内角,且tanA, tanB是方程6x2-5x+1=0的两个实数根,那么,△ABC是( )
A.钝角三角形 B.锐角三角形 C.等腰三角形 D.等边三角形
联想:(1)△ABC中,tanA=
 , 边C=1,则最短边长为 。
, 边C=1,则最短边长为 。(2)△ABC中,tanA=
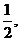 tanB=-2,△ABC的面积为1,则三边长为a=____________, b=___________, c=__________________
tanB=-2,△ABC的面积为1,则三边长为a=____________, b=___________, c=__________________(3)△ABC中,三内角A,B,C的所对的边分别为a,b,c,已知B是A与C的等差中项,a+
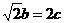 ,则sin
C=_________________.
,则sin
C=_________________.(4) 在锐角△ABC中,a,b,c,分别为角A,B,C的对边,A<B<C,B=60°,而且
 ,求①A,B,C,的大小;②
,求①A,B,C,的大小;②  的值。
的值。(5)已知:sin 2
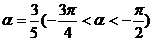 ,函数f(x)=sin(
,函数f(x)=sin( )-sin(
)-sin(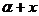 )+2cos
)+2cos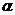 .①求cos
.①求cos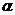 的值;②若f-1(x)表示f (x) 在[
的值;②若f-1(x)表示f (x) 在[ ]上的反函数,试求f-1(
]上的反函数,试求f-1( )的值。
)的值。 -
6.A.P{an}中,an-1-a
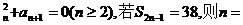 (
)
(
)A.38 B.20 C.10 D.9
联想:(1)已知Sk表示数列{an}的前K项的和,且SK+1+SK=ak+1(K
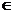 N),那么此数列是(
)
N),那么此数列是(
)A.递增数列 B.递减数列 C.常数列 D.摆动数列
(2)在G.P{an}中,对任意自然数n, 有a1+a2+…+an=2n-1,则a12+a22…+a
 ________(
)
________(
)A.4n-1 B.
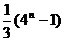 C.
C.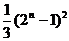 D.(2n-1)2
D.(2n-1)2(3) .A.P{an}中,已知公差d=1, 前98项和S98=137,则a2+a4+…+a96+a98=______________
(4) 数列{an}满足a1=
 ,a1+a2+…+an=n2 .an, 则数列{an}的通项公式为
.
,a1+a2+…+an=n2 .an, 则数列{an}的通项公式为
.(5){an}、{bn}都是各项为正的数列,对任意的自然数n,都有an , b
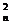 ,
an+1成等差数列,b
,
an+1成等差数列,b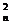 ,
an+1,
,
an+1,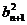 成等比数列。
成等比数列。①试问{bn}是否为A、P?为什么?②求证:对任意的自然数p、q(p>q),
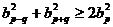 成立;③如果a1 = 1 , b1 =
成立;③如果a1 = 1 , b1 =  ,
Sn =
,
Sn =  , 求
, 求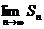
-
7.已知目标函数z = 5x + y且变量x、y满足下列条件
 ,则zmax为( )
,则zmax为( )A.23 B.27 C.28 D.29
联想:(1)已知集合A={
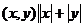 ≤
≤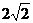 },B={
},B={ x2-y2≥0},M=A
x2-y2≥0},M=A B,则M的面积为( )
B,则M的面积为( )A.16 B.
 C.8
D.
C.8
D.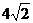
(2)三边的长都是整数,且最大边长为9的三角形的个数是 。
(3)已知△ABC的三边长a、b、c满足b + c≤2a , c + a≤2b , 则
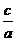 的取值范围为 。
的取值范围为 。(4)某企业要安装A种电子设备45台,B种电子设备50台,需用白铁皮给每台装配一个外壳,已知白铁皮有两种规格:甲种每张面积为2m2,每张可做A品外壳3个和B的外壳5个,乙种每张面积3m2,可做A的外壳6个和B的外壳5个,当总用料面积最小时,甲种用了 张,乙种用了 张。
-
8.设的
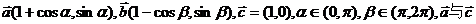 的夹角为θ1,
的夹角为θ1,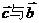 的夹角为θ2,且θ1-θ2 =
的夹角为θ2,且θ1-θ2 = 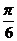 ,则
,则 的值为
。
的值为
。联想:已知两点M(-1,0),N(1,0),且点P使
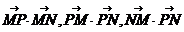 成公差小于零的等差数列。(Ⅰ)求点P的轨迹是什么曲线?(Ⅱ)若点P的坐标是(x0 , y0),θ为
成公差小于零的等差数列。(Ⅰ)求点P的轨迹是什么曲线?(Ⅱ)若点P的坐标是(x0 , y0),θ为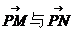 的夹角,求tanθ。
的夹角,求tanθ。 -
9.已知双曲线
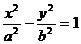 (a>0,b>0)的离心率为
(a>0,b>0)的离心率为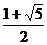 ,A、F分别是它的左顶点和右焦点,点B(0,b),则∠ABF等于(
)
,A、F分别是它的左顶点和右焦点,点B(0,b),则∠ABF等于(
)A.1200 B.600 C.1500 D.900
联想:(1)已知椭圆
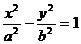 (a > 0 , b > 0)的左、右两焦点分别为F1、F2,以F1为顶点,F2为焦点的抛物线经过椭圆的顶点(即(0,±b)),则椭圆的离心率为
。
(a > 0 , b > 0)的左、右两焦点分别为F1、F2,以F1为顶点,F2为焦点的抛物线经过椭圆的顶点(即(0,±b)),则椭圆的离心率为
。(2)已知点F(
 ,0),直线
,0),直线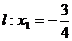 ,点B是直线
,点B是直线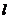 上动点,若过点B垂直于y轴的直线与线段BF的垂直平分线交于点M,则点M的轨迹是(
)
上动点,若过点B垂直于y轴的直线与线段BF的垂直平分线交于点M,则点M的轨迹是(
)A.双曲线 B.椭圆 C.圆 D.抛物线
(3)设圆过双曲线
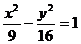 的一个顶点和一个焦点,圆心在此双曲线上,则圆心到双曲线中心的距离是
。
的一个顶点和一个焦点,圆心在此双曲线上,则圆心到双曲线中心的距离是
。(4)已知椭圆C:
 (a >b > 0)的两个焦点分别为F1、F2,斜率为k的直线
(a >b > 0)的两个焦点分别为F1、F2,斜率为k的直线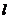 过右焦点F2,且与椭圆交于A、B两点,与y轴交于M点,且点B分
过右焦点F2,且与椭圆交于A、B两点,与y轴交于M点,且点B分 的比为2。①若
的比为2。①若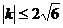 ,求离心率e的取值范围。②若
,求离心率e的取值范围。②若 ,并且弦AB的中点到右准线的距离为
,并且弦AB的中点到右准线的距离为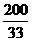 ,求椭圆的方程。
,求椭圆的方程。 -
10.甲烷分子由一个碳原子和四个氢原子组成,其空间构型为一个正四面体,碳原子位于该正四面体的中心,四个氢原子均视为一个点(体积忽略不计),且已知碳原子与每个氢原子间的距离都为a,则以四个氢原子为顶点的这个正四面体的体积为( )
A.
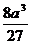 B.
B.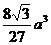 C.
C. D.
D.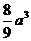
联想:(1)一个三棱锥的三个侧,面中有两个是等腰直角三角形,另一个边长为1的正三角形,这样的三棱锥体积为 。(写出一个可能值)
(2)设长方体的三条棱长分别为a、b、c,若长方体所有棱的长度之和为24,一条对角线长度为5,体积为2,则
 等于(
)
等于(
)A.
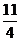 B.
B.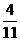 C.
C. D.
D.
(3)把边长为a的正方形ABCD,沿对角线AC折成600的二面角,这时顶点B到CD的距离是( )
A.a B.
 C.
C.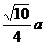 D.
D.
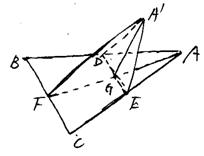
(4)已知边长为a的正三角形ABC的中线AF与中位线DE相交于G,将此三角形沿DE折成二面角A′-DE-B。(Ⅰ)求证:平面A′GF⊥平面BCED。(Ⅱ)当二面角A′-DE-B为多大时,异面直线A′E与BD互相垂直?证明你的结论?
-
11.市场营销人员对过去几年某商品的价格及销售数量的关系作数据分析发现有如下规律:该商品的价格每上涨x%(x > 0),销售数量就减少kx%(其中k为正常数)。目前,该商品定价为a元,统计其销售数量为b个。
(Ⅰ)当k=
 时,该商品的价格上涨多少,就能使销售的总金额达到最大?(Ⅱ)在适当的涨价过程中,求使销售总金额不断增加时,k的取值范围。
时,该商品的价格上涨多少,就能使销售的总金额达到最大?(Ⅱ)在适当的涨价过程中,求使销售总金额不断增加时,k的取值范围。 -
12.已知函数f ( x )的定义域为D,若存在x0
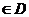 ,使f ( x0 ) = x0 ,则称点是函数f
( x )的不动点。(Ⅰ)若f ( x )=
,使f ( x0 ) = x0 ,则称点是函数f
( x )的不动点。(Ⅰ)若f ( x )=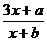 有两个关于原点对称的不动点,求实数a、b应满足的条件;(Ⅱ)在(Ⅰ)的条件下,若a = 8,记f ( x )的两个不动点为A、B,P为f ( x )图象上的点,其纵坐标yp>3,求点P到直线AB的距离的最小值及点P。
有两个关于原点对称的不动点,求实数a、b应满足的条件;(Ⅱ)在(Ⅰ)的条件下,若a = 8,记f ( x )的两个不动点为A、B,P为f ( x )图象上的点,其纵坐标yp>3,求点P到直线AB的距离的最小值及点P。
高考数学最后冲刺训练 联想与激活(5)参考答案
[参考答案]
联想与激活(5)
1.C 联想:(1)A
(2)y = -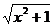 (x≥0) (3)9
(x≥0) (3)9
(4)t≤ (5)D
(6)C
(5)D
(6)C
2.C 联想:(1)①②③ (2)a
=  (3)A
(4)
(3)A
(4)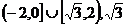
3.B 联想:(1)B (2)A (3)4 (4)12
4.A 联想:(1)C (2)x+y
= 3 (3)y2-x2
= 
(4)-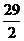 (5)
(5)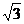 ,1200
(6)-34
,1200
(6)-34
5.B 联想:(1)B (2) (3)
(3)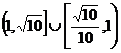
6.A 联想:(1)A (2)3 (3)A (4)D
7.D 联想:(1)A (2)B
(3)C (4)-3x4-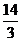 x3
(5)[ 1,
x3
(5)[ 1, ]
]
8.B 联想:(1)B (2)10 (3)C
9.C 联想:(1)1 (2)8
10.C 联想: D
11. 2联想:(1)( x-1)2 = 4(y+1) (2)( y+6 )2 = 8(x+6)
12.解:(I)设F(C,O)(C>O) C=
C= 又b=1,
∴a=3
又b=1,
∴a=3
∴
(II)假设这样的直线存在,交于两点(x1,y1)(x2,y2)
则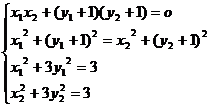
利用中点在椭圆的内部求出k的范围是(-1,0)∪(0,1)
联想与激活(6)
1.B
联想:(1) (2)B (3)C
(2)B (3)C
2.B 联想:(1)B (2)0<a<1时,x>1;a>1时,0<x<1
(3)a>1时,x∈(-1,0);0<a<1时,x∈(-2,-1)
3.A 联想:(1)D (2)A (3)C (4)m>7
4.B
联想:(1)D (2)cos4x或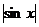 (3)f
(m-1)>0
(3)f
(m-1)>0
5.A
联想:(1)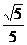 (2)
(2) (3)
(3)
(4)①A=45°,B=60°,C=75°
②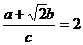
设A=60°-α,C=60°+α
 =2cosAcosC=cos(A+C)+cos(A-C)=cos120°+cos2α=
=2cosAcosC=cos(A+C)+cos(A-C)=cos120°+cos2α=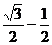
∴cos2α=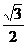 α=15°
∴A=45°,C=75°
α=15°
∴A=45°,C=75°

(5) ①cosa= ②f-1(
②f-1( )=
)=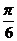
2a ∴cos2
∴cos2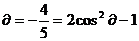
2cos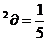 cos
cos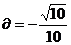
f(x)=-2cos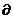 sinX+2cos
sinX+2cos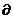 ∴-2cos
∴-2cos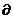 sinx+2cos
sinx+2cos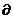 =-
=-
∴-2sinx+2=1
sinx= x=
x=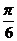 f-1(-
f-1(- )=
)=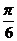
6. C 联想:(1)C (2)B (3)93
(4)an= (5) ①{bn}为A.P
(5) ①{bn}为A.P
bn≠o,
2b anan+1, an+1=bnbn+1,an=bn-1bn
anan+1, an+1=bnbn+1,an=bn-1bn
∴2b bn(bn-1+bn+1)
2bn = bn-1+bn+1
bn(bn-1+bn+1)
2bn = bn-1+bn+1
②2b
③3 a1+a2=2b ∴a2=3
a2=b1b2 b2=
∴a2=3
a2=b1b2 b2=
∴d= ∴bn=
∴bn= n ∴an=bn-1bn=
n ∴an=bn-1bn= (n-1).
(n-1). n=
n= (n≥2)
(n≥2)
∴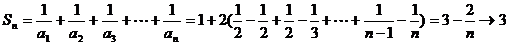
7.B
联想:(1)C (2)19
(3)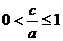 (4)5,5
(4)5,5
8.- 联想:I.圆
II.
联想:I.圆
II.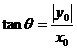
设p(x,y)  =2x+2
=2x+2
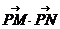 =x2-1+y2
=x2-1+y2
 ∴2x=x2-1+y2
(x-1)2+y2=2
∴2x=x2-1+y2
(x-1)2+y2=2

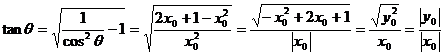 (x0≥0)
(x0≥0)
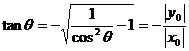 (x0<0
(x0<0 ∴
∴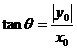
9.D
联想:(1)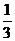 (2)D
(3)
(2)D
(3)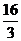 (4)
(4) ≤e<1
≤e<1

①B(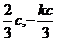 )
∴
)
∴ ∴4e4-37e2+9≤0
∴4e4-37e2+9≤0
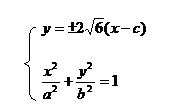
 ≤e≤3又e<1
∴
≤e≤3又e<1
∴ ≤e≤1
≤e≤1
②e=

 ∴
∴ a=4
a=4
∴
10.B
联想:(1) (答案不唯一) (2)A (3)B
(答案不唯一) (2)A (3)B
(4)I:证:正△ABC中,作BC边上高AF,交BC于F
交DE于G,则AG⊥DE,DE⊥FG。
∴A′G⊥DE,FG⊥DE A′G交FG于面A′GF ∴面DE⊥A′GF
DE 面BCED
∴面A′GF⊥面BCED
面BCED
∴面A′GF⊥面BCED
Ⅱ:过A′作A′M⊥AF于M,连EM。
面A′GF⊥面BCED A′M⊥AF 易知A′M⊥面ABC 又A′E⊥BD
∴EM⊥AB 则AM=2MG 如图
 A′G = AG =
3MG ∴cos∠A′GM
=
A′G = AG =
3MG ∴cos∠A′GM
= 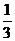
∠A′GM
= π-arccos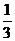
A′G⊥DE , FG⊥DE ∴∠A′GF为所求二面角的平面角
∴所求二面角为π-arccos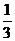
11.Ⅰ:总金额 y = a.( 1+ x% ). b ( 1- x%)
x%)
y =  ab (1+x%
) ( 2-x% )≤
ab (1+x%
) ( 2-x% )≤ ab.(
ab.(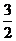 )2
1+x% = 2-x% 时“=”成立
)2
1+x% = 2-x% 时“=”成立
x% =  =
50% 价格上涨50%
=
50% 价格上涨50%
Ⅱ:y = ab( 1+ x% ) ( 1-kx%) y = ab[-k (x% )2+( 1-k) x%+1 ]
∴y′
= ab.[(-2k)x% . +(
1-k)
+(
1-k)  ] > 0 恒成立时
] > 0 恒成立时
说明y是不断递增 ∴0<k<1
12.Ⅰ:设不动点(x0 , x0)(-x0 , -x0)

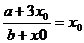 a = x02
b = 3
a = x02
b = 3
满足a > 0 且a≠9 b = 3
Ⅱ: a = 8
f ( x ) = 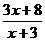
 :y = x
:y = x
p ( xp , 3-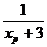 )
3-
)
3-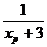 > 3 xp
<-3
> 3 xp
<-3
d =  .
. xp+3
< 0
xp+3
< 0
∴ d =  .(
.(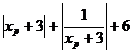 )≥
)≥ .(2+6)=
4
.(2+6)=
4
xp+3
= -1时 即xp = -4时
dmin = 4 , P(-4 , 4)
, P(-4 , 4)