-
(1)熟练掌握函数y=Asin(ωx+
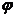 )(A>0,ω>0)的图象及其性质,以及图象的五点作图法、平移和对称变换作图的方法.
)(A>0,ω>0)的图象及其性质,以及图象的五点作图法、平移和对称变换作图的方法.(2)利用单位圆、函数的单调性或图象解决与三角函数有关的不等式问题.
(3)各类三角公式的功能:变名、变角、变更运算形式;注意公式的双向功能及变形应用;用辅助角的方法变形三角函数式.
[注意]近年的高考题中,三角函数主要考查基础知识、基本技能、基本方 法,一般都在选择题与填空题中考查,多为容易或中等难度的题目.其中,同角三角函数的 基本公式和诱导公式,三角函数的图像和性质,求三角函数式的值等为考查热点.
-
1.常见三角不等式
(1)若
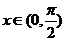 ,则
,则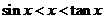 .
.(2) 若
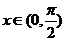 ,则
,则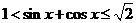 .
.(3)
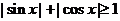 .
. -
2.同角三角函数的基本关系式
 ,
,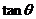 =
=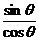 ,
,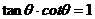 .
. -
3.正弦、余弦的诱导公式
(1)负角变正角,再写成2k
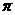 +
+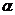 ,
,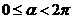 ;
;(2)转化为锐角三角函数。
-
4.


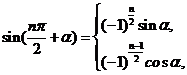
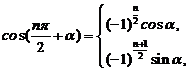 和角与差角公式
和角与差角公式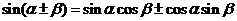 ;
; ;
; .
.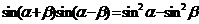 (平方正弦公式);
(平方正弦公式);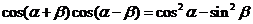 .
. =
=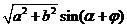 (辅助角
(辅助角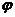 所在象限由点
所在象限由点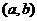 的象限决定,
的象限决定,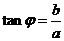 ).
). -
5.二倍角公式
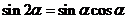 .
.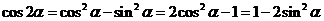
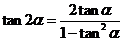 .
. -
7.三角函数的周期公式
函数
 ,x∈R及函数
,x∈R及函数 ,x∈R(A,ω,
,x∈R(A,ω,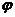 为常数,且A≠0,ω>0)的周期
为常数,且A≠0,ω>0)的周期 ;函数
;函数 ,
,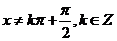 (A,ω,
(A,ω,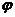 为常数,且A≠0,ω>0)的周期
为常数,且A≠0,ω>0)的周期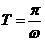 .
.性质
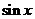
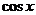
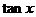
图像的来源
及图像
定义域
值域
单调性及
递增递减区间
周期性及
奇偶性
对称轴
对称中心
最值及指定区间的最值
简单三角方程和不等式
30°
45°
60°
0°
90°
180°
270°
15°
75°

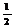
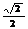

0
1
0
-1
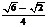
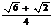
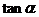

1
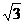
0
0
2- 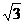
2+ 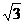
-
8.正弦定理
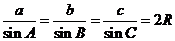 .9.余弦定理
.9.余弦定理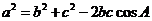 ;
;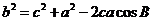 ;
;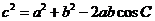 .
. -
10.面积定理
(1)
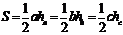 (
(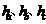 分别表示a、b、c边上的高).
分别表示a、b、c边上的高).三基本概念
1象限角的概念:如果角的终边在坐标轴上,就认为这个角不属于任何象限。
-
2.弧长公式:
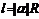 ,扇形面积公式:
,扇形面积公式: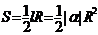 ,1弧度(1rad)
,1弧度(1rad)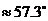 .
. -
3、任意角的三角函数的定义:设
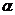 是任意一个角,P
是任意一个角,P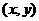 是
是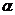 的终边上的任意一点(异于原点),
的终边上的任意一点(异于原点),它与原点的距离是
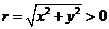 ,那么
,那么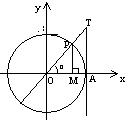
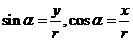 ,
,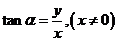 ,
,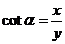
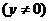
-
4.三角函数线的特征是:正弦线MP“站在
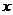 轴上(起点在
轴上(起点在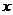 轴上)”、余弦线OM“躺在
轴上)”、余弦线OM“躺在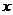 轴上(起点是原点)”、正切线AT“站在点
轴上(起点是原点)”、正切线AT“站在点 处(起点是
处(起点是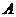 )”.三角函数线的重要应用是比较三角函数值的大小和解三角不等式。
)”.三角函数线的重要应用是比较三角函数值的大小和解三角不等式。 -
5.特殊角的三角函数值:
-
6.三角函数的恒等变形的基本思路是:一角二名三结构。即首先观察角与角之间的关系,注意角的一些常用变式,角的变换是三角函数变换的核心!第二看函数名称之间的关系,通常“切化弦”;第三观察代数式的结构特点。基本的技巧有:
(1)巧变角如(2)三角函数名互化(切割化弦),
(3)公式变形使用(4)三角函数次数的降升,
(5)式子结构转化(对角、函数名、式子结构化同)。
(6)常值变换主要指“1”的变换
(7)正余弦“三兄妹-
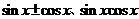 ”的内存联系――“知一求二”,
”的内存联系――“知一求二”, -
7、辅助角公式中辅助角的确定:
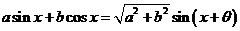 (其中
(其中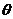 角所在的象限由a, b的符号确定,
角所在的象限由a, b的符号确定,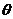 角的值由
角的值由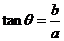 确定)在求最值、化简时起着重要作用。
确定)在求最值、化简时起着重要作用。 -
8、形如
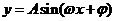 的函数:
的函数:(1)几个物理量:A―振幅;
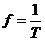 ―频率(周期的倒数);
―频率(周期的倒数); ―相位;
―相位;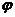 ―初相;
―初相;(2)函数
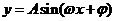 表达式的确定:A由最值确定;
表达式的确定:A由最值确定;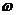 由周期确定;
由周期确定;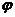 由图象上的特殊点确定,
由图象上的特殊点确定,(3)函数
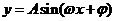 图象的画法:①“五点法”――设
图象的画法:①“五点法”――设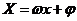 ,令
,令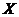 =0,
=0,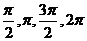 求出相应的
求出相应的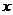 值,计算得出五点的坐标,描点后得出图象;②图象变换法:这是作函数简图常用方法。
值,计算得出五点的坐标,描点后得出图象;②图象变换法:这是作函数简图常用方法。 -
9.研究函数
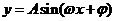 性质的方法:类比于研究
性质的方法:类比于研究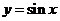 的性质,只需将
的性质,只需将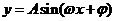 中的
中的 看成
看成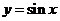 中的
中的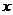 ,但在求
,但在求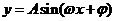 的单调区间时,要特别注意A和
的单调区间时,要特别注意A和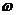 的符号,通过诱导公式先将
的符号,通过诱导公式先将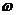 化正。
化正。 -
10.反三角函数:
(1)反三角函数的定义(以反正弦函数为例):
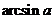 表示一个角,这个角的正弦值为
表示一个角,这个角的正弦值为 ,且这个角在
,且这个角在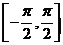 内
内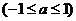 。
。(2)反正弦
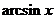 、反余弦
、反余弦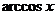 、反正切
、反正切 的取值范围分别是
的取值范围分别是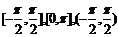 .
. -
20、求角的方法:先确定角的范围,再求出关于此角的某一个三角函数(要注意选择,其标准有二:一是此三角函数在角的范围内具有单调性;二是根据条件易求出此三角函数值)。