-
(1)理解不等式的性质及其证明.
(2)掌握两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理,并会简单的应用.
(3)掌握分析法、综合法、比较法证明简单不等式.
(4)掌握简单不等式的解法.
(5)理解│a│-│b│≤│a+b│≤│a│+│b│
[注意]不等式在数学的各个分支中都有广泛的应用,同时还是继续学习高等数学的基础.纵观历年试题,涉及不等式内容的考题大致可分为以下几类:①不等式的证明;②解不等式;③取值范围的问题;④应用题.
-
1.常用不等式:
(1)
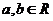
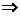
 (当且仅当a=b时取“=”号).
(当且仅当a=b时取“=”号).(2)
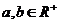
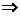
 (当且仅当a=b时取“=”号).
(当且仅当a=b时取“=”号).(3)

(4)柯西不等式

(5)
 .
. -
2.极值定理
已知
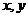 都是正数,则有
都是正数,则有(1)若积
 是定值
是定值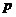 ,则当
,则当 时和
时和 有最小值
有最小值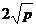 ;
;(2)若和
 是定值
是定值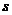 ,则当
,则当 时积
时积 有最大值
有最大值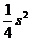 .
. -
3.一元二次不等式
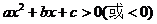
 ,
,如果
 与
与 同号,则其解集在两根之外;如果
同号,则其解集在两根之外;如果 与
与 异号,则其解集在两根之间.简言之:同号两根之外,异号两根之间.
异号,则其解集在两根之间.简言之:同号两根之外,异号两根之间.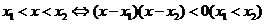 ;
; .
. -
4.含有绝对值的不等式 当a> 0时,有
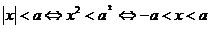 .
. 或
或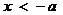 .
. -
5.指数不等式与对数不等式
(1)当
 时,
时,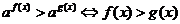 ;
; 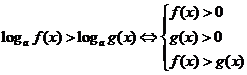 .
.(2)当
 时,
时,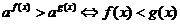 ;
;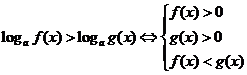
-
1、不等式的性质:
(1)同向不等式可以相加;异向不等式可以相减:若
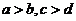 ,则
,则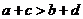 (若
(若 ,则
,则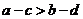 ),但异向不等式不可以相加;同向不等式不可以相减;
),但异向不等式不可以相加;同向不等式不可以相减;(2)左右同正不等式:同向的不等式可以相乘,但不能相除;异向不等式可以相除,但不能相乘:若
 ,则
,则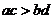
若
 ,则
,则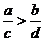 ;
;(3)左右同正不等式:两边可以同时乘方或开方:若
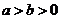 ,则
,则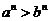 或
或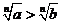 ;
;(4)若
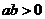 ,
,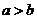 ,则
,则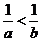 ;若
;若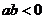 ,
,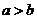 ,则
,则 。
。 -
2. 不等式大小比较的常用方法:(1)作差:作差后通过分解因式、配方等手段判断差的符号得出结果;(2)作商(常用于分数指数幂的代数式);(3)分析法;(4)平方法;(5)分子(或分母)有理化;(6)利用函数的单调性;(7)寻找中间量或放缩法 ;(8)图象法。其中比较法(作差、作商)是最基本的方法。
-
3.利用重要不等式求函数最值时,你是否注意到:“一正二定三相等,和定积最大,积定和最小”这17字方针。
-
4.常用不等式有:
(1)
 (根据目标不等式左右的运算结构选用) ;
(根据目标不等式左右的运算结构选用) ;(2)a、b、c
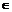 R,
R,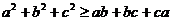 (当且仅当
(当且仅当 时,取等号);
时,取等号);(3)若
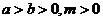 ,则
,则 (糖水的浓度问题)。
(糖水的浓度问题)。 -
5、证明不等式的方法:比较法、分析法、综合法和放缩法(比较法的步骤是:作差(商)后通过分解因式、配方、通分等手段变形判断符号或与1的大小,然后作出结论。).
常用的放缩技巧有:

-
6.简单的一元高次不等式的解法:
标根法:(1)分解成若干个一次因式的积,并使每一个因式中最高次项的系数为正;
(2)将每一个一次因式的根标在数轴上,从最大根的右上方依次通过每一点画曲线;并注意奇穿过偶弹回;
(3)根据曲线显现
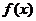 的符号变化规律,写出不等式的解集。
的符号变化规律,写出不等式的解集。 -
7.分式不等式的解法:分式不等式的一般解题思路是先移项使右边为0,再通分并将分子分母分解因式,并使每一个因式中最高次项的系数为正,最后用标根法求解。解分式不等式时,一般不能去分母,但分母恒为正或恒为负时可去分母。
-
8.绝对值不等式的解法:
(1)分段讨论法(最后结果应取各段的并集):
(2)利用绝对值的定义;
(3)数形结合
-
9、含参不等式的解法:求解的通法是“定义域为前提,函数增减性为基础,分类讨论是关键.”注意解完之后要写上:“综上,原不等式的解集是…”。注意:按参数讨论,最后应按参数取值分别说明其解集;但若按未知数讨论,最后应求并集.
提醒:(1)解不等式是求不等式的解集,最后务必有集合的形式表示;
(2)不等式解集的端点值往往是不等式对应方程的根或不等式有意义范围的端点值。
-
11.含绝对值不等式的性质:
 同号或有
同号或有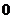

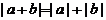
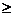
 ;
; 异号或有
异号或有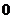

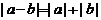
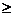
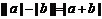 .
. -
12.不等式的恒成立,能成立,恰成立等问题:不等式恒成立问题的常规处理方式?(常应用函数方程思想和“分离变量法”转化为最值问题,也可抓住所给不等式的结构特征,利用数形结合法)
1).恒成立问题
若不等式
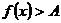 在区间
在区间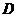 上恒成立,则等价于在区间
上恒成立,则等价于在区间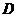 上
上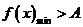
若不等式
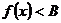 在区间
在区间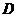 上恒成立,则等价于在区间
上恒成立,则等价于在区间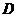 上
上
(1)设实数
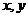 满足
满足 ,当
,当 时,
时, 的取值范围是______
的取值范围是______(答:
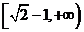 );
);(2)不等式
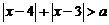 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数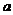 的取值范围_____
的取值范围_____(答:
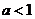 );
);(3)若不等式
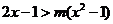 对满足
对满足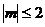 的所有
的所有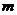 都成立,则
都成立,则 的取值范围_____
的取值范围_____(答:(
 ,
,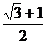 ));
));(4)若不等式
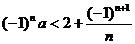 对于任意正整数
对于任意正整数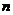 恒成立,则实数
恒成立,则实数 的取值范围是_____(答:
的取值范围是_____(答: );
);(5)若不等式
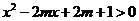 对
对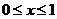 的所有实数
的所有实数 都成立,求
都成立,求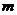 的取值范围.(答:
的取值范围.(答: )
)2). 能成立问题
若在区间
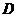 上存在实数
上存在实数 使不等式
使不等式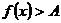 成立,则等价于在区间
成立,则等价于在区间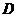 上
上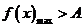 ;
;若在区间
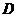 上存在实数
上存在实数 使不等式
使不等式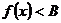 成立,则等价于在区间
成立,则等价于在区间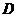 上的
上的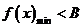 .
.已知不等式
 在实数集
在实数集 上的解集不是空集,求实数
上的解集不是空集,求实数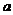 的取值范围______
的取值范围______(答:
 )
)3). 恰成立问题
若不等式
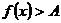 在区间
在区间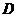 上恰成立, 则等价于不等式
上恰成立, 则等价于不等式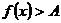 的解集为
的解集为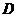 ;
;若不等式
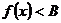 在区间
在区间 上恰成立, 则等价于不等式
上恰成立, 则等价于不等式