1．下面四个手机应用图标中，属于中心对称图形的是　　 (　　 )

A　　　　　　　　 B　　　　　　 　　　C　　　　　　　　　 D

2．若方程(a-2)x²-2017x+2018=0是关于x的一元二次方程，则　　 (　　 )

　 A．a≠1　　 B．a≠-2　　 C．a≠2　　 D．a≠3

3．抛物线y=-(x-4)²-3的顶点坐标是　　 (　　 )

　 A．(-4．3)　　 B．(-4．-3)　　 C．(4，3)　　 D．(3，4)

4．方程x²-9=0的解是　　 (　　 )

　 A．X=3　　 B．X=-3　　 C．X1=3,X2=-3　　 D．X=±9

5．已知,AB是⊙O的弦,且AB=OA，则∠0AB的度数为　　 (　　 )

6．在平面直角坐标系中，点A(a,-b)关于原点对称的点的坐标为　　 (　　 )

　 A．(-a，-b)　　 B．(a，b)　　 C．(-a，b)　　 D．(a，-b)

7．下列关于X的一元二次方程2X²-mX-1=0根的情况判定正确的是　　 (　　 )

　 A．有两个不相等的实数根　　 B．有两个相等的实数根

　 C．没有实数根　　　　　　　 D．无法判断

8．已知抛物线y=aX²+2017(a>o)过A(，y1)、B(，y2)两点．则下列关系式一定正确的是　　 (　　 )

　 A. y1>0>y2　　 B．y2>0>y1　　 C．y1>y2>0　 D．y2>y1>0

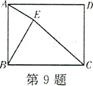
9．如图．在矩形ABCD中，AB=4，BC=6．E是矩形内部的一个动点，且AE⊥BE，则线段CE的最小值为　　 (　　 )

　 A．　　 B．2-2　　 C．2-2　 D．4

10．如图，已知抛物线y=aX²+bX+c(a≠0)的对称轴为直线X=1，与X轴的一个交点坐标为(-1，0)，其部分图象如图所示。下列结论：①方程=aX²+bX+c=0的两个根是X1=-1，X2=3：②a-b+c=0；③8a+c<0；④当y>0时,X的取值范围是-1<X<3；⑤当y随X的增大而增大时，一定有X<O。其中结论正确的个数是　　 (　　 )

　 A．1个　　 B．2个　　 C．3个　　 D．4个

11．已知一元二次方程X²-2X-2=0的两个实数根为X1，X2．则X1X2-X1-X2的值是_______．

12．二次函数y=X²+bX+c的图象上有两点A(-1,)．B(3,)，则此抛物线的对称轴是直线X=_________．

13．如图,点A、B、C为⊙0上的三个点,∠BOC=2∠AOB．∠ACB=15°．则∠ABC=__________度．

14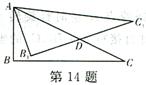．如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°．将△ABC绕点A按逆时针方向旋转15°后得到△AB1C1,B1C1交AC于点D，如果AD=4，

则△ABC的面积等于________．

15．解方程：X²-4X-12=0

16．2017年5月14日---5月15日．“一带一路”国际合作高峰论坛在北京成功举办，高峰论坛期间及前夕，各国政府、地方、企业等达成一系列合作共识、重要举措及务实成果。中方对其中具有代表性的一些成果进行了梳理和汇总，形成高峰论坛成果清单。清单主要涵盖政策沟通、设施联通、贸易畅通、资金融通、民心相通5大类，共76大项、270多项具体成果。我市新能源产业受这一利好因素，某企业的利润逐月提高。据统计，2017年第一季度的利润为2000万元，第三季度的利润为2880万元．

　 (1)求该企业从第一季度到第三季度利润的平均增长率；

　 (2)若第四季度保持前两季度利润的平均增长率不变，该企业2017年的年利润总和能否突破1亿元?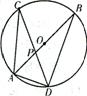

17．如图，在⊙0中，直径AB与弦CD相交于点P，∠CAB=45°，∠B=20°。

　 (1)求∠APD的大小；

　 (2)已知AD=4，求圆心O到BD的距离是多少?

18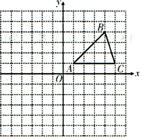．在平面直角坐标系中，△ABC的位置如图所示(每个小方格都

　 是边长为1个单位长度的正方形)．

　 (1)将△ABC沿Y轴方向向下平移5个单位长度,画出平移后

　　 得到的△A1B1C1：

　 (2)将△ABC绕着点A逆时针旋转90°，画出旋转后得到的

　　 △AB2C2．并直接写出点B2、C2的坐标．

19．下表给出了代数式-X²+bX+c与X的一些对应值：

(1)根据表格中的数据，确定b,c和m的值；

(2)设y=-X²+bX+c，直接写出当-1≤X≤3时，y的最小值

20．某团购网站的商品进价为每件60元，售价为每件100元时，每天可卖出120件；如果每件商品的售价每上涨1元，则每天少卖2件，设每件商品的售价为X元(X为正整数)，每天的销售利润为y元．

　 (1)当每件商品的售价是多少元时，每天的利润刚好是4800元?

　 (2)当每件商品的售价定为多少元时．每天可获得最大利润?最大的利润是多少元?

21．如图，在等边三角形ABC中，点D为△ABC内的一点，∠ADB=120°，∠ADC=90°，将△ABD绕点A逆时针旋转60°，得△ACE，连接DE．

　 (1)求证：AD=DE；

　 (2)求∠DCE的度数；

　 (3)若BD=1，求AD，CD的长．

22．如图．AB为⊙0的直径，点E在⊙O上，点C为BE弧的中点，过点C作

　 直线CD⊥AE于点D，连接AC、BC．

　 (1)证明：直线CD是⊙0的切线；　

　 (2)若点E是AD的中点，且AD=2，AC=．求AB的长．

23．如图，抛物线y=aX2+bX-3(a≠0)与X轴交于点A(1,0)和点B,与y轴交于点C,且其对称轴l为直线X=-1,点P是抛物线上B，C之间的一个动点(点P不与点B，C重合)．

　 (1)求抛物线的解析式：

　 (2)求四边形PBAC面积的最大值，并求出此时点P的坐标。

　 (3)将抛物线y=aX2+bX-3向上平移m(m>0)个单位长度得到新的抛物线,新的抛物线与直线