16. 如图所示,两个物体以相同大小的初始速度从空中O点同时分别向x轴正负方向水平抛出,它们的轨迹恰好是抛物线方程y=$\frac{1}{k}$x2,重力加速度为g,那么以下说法正确的是(曲率半径可认为等于曲线上该点的瞬时速度所对应的匀速率圆周运动的半径)( )
如图所示,两个物体以相同大小的初始速度从空中O点同时分别向x轴正负方向水平抛出,它们的轨迹恰好是抛物线方程y=$\frac{1}{k}$x2,重力加速度为g,那么以下说法正确的是(曲率半径可认为等于曲线上该点的瞬时速度所对应的匀速率圆周运动的半径)( )
 如图所示,两个物体以相同大小的初始速度从空中O点同时分别向x轴正负方向水平抛出,它们的轨迹恰好是抛物线方程y=$\frac{1}{k}$x2,重力加速度为g,那么以下说法正确的是(曲率半径可认为等于曲线上该点的瞬时速度所对应的匀速率圆周运动的半径)( )
如图所示,两个物体以相同大小的初始速度从空中O点同时分别向x轴正负方向水平抛出,它们的轨迹恰好是抛物线方程y=$\frac{1}{k}$x2,重力加速度为g,那么以下说法正确的是(曲率半径可认为等于曲线上该点的瞬时速度所对应的匀速率圆周运动的半径)( )| A. | 初始速度为$\sqrt{2kg}$ | B. | 初始速度为$\sqrt{kg}$ | ||
| C. | O点的曲率半径为$\frac{k}{2}$ | D. | O点的曲率半径为2k |
12.利用如图1所示的实验装置探究“加速度a与力F及物体质量M的定量关系”.其中,A为小车,B为打点计时器,C为装有砂的砂桶(总质量为m),D为一端带有定滑轮的长木板(实验时已经平衡了摩擦力).

(1)若保持砂和砂桶的质量不变,改变小车的质量M,分别得到小车加速度a与质量M及对应的$\frac{1}{M}$数据如表所示:
①根据表数据,为了反映F不变时a与M的关系,请在图2所示的方格坐标纸中选择恰当的物理量建立坐标系,并作出图象.
②根据图线得出F不变时a与M的关系是a与M成反比.
(2)小车质量一定,探究加速度a与F的关系时,某同学根据测量记录的数据,作出图象如图3所示.
①根据图象得到的结论是在质量一定的情况下,物体的加速度与物体所受的合外力成正比.
②图象斜率的物理意义是物体质量的倒数$\frac{1}{m}$.
③在实验中,我们认为细线的拉力F等于砂桶的重力,实际上细线的拉力F小于砂桶的重力mg(填“大于”“小于”或“等于”).

(1)若保持砂和砂桶的质量不变,改变小车的质量M,分别得到小车加速度a与质量M及对应的$\frac{1}{M}$数据如表所示:
| 序号 | 1 | 2 | 3 | 4 | 5 |
| 小车的加速度a/(m•s-2) | 1.98 | 1.48 | 1.00 | 0.67 | 0.50 |
| 小车质量M/kg | 0.25 | 0.33 | 0.50 | 0.75 | 1.00 |
| 质量倒数$\frac{1}{M}$/kg-1 | 4.00 | 3.00 | 2.00 | 1.33 | 1.00 |
②根据图线得出F不变时a与M的关系是a与M成反比.
(2)小车质量一定,探究加速度a与F的关系时,某同学根据测量记录的数据,作出图象如图3所示.
①根据图象得到的结论是在质量一定的情况下,物体的加速度与物体所受的合外力成正比.
②图象斜率的物理意义是物体质量的倒数$\frac{1}{m}$.
③在实验中,我们认为细线的拉力F等于砂桶的重力,实际上细线的拉力F小于砂桶的重力mg(填“大于”“小于”或“等于”).
11.如图1所示是用打点计时器测瞬时速度实验时得到的一条纸带的一部分,从0点开始依照打点的先后依次标为0、1、2、3、4、5、6,现在量得0、1间的距离x1=5.18cm,1、2间的距离x2=4.40cm,2、3间的距离x3=3.62cm,3、4间的距离x4=2.78cm,4、5间的距离x5=2.00cm,5、6间的距离x6=1.22cm (f=50Hz)

①据上面记录,计算打点计时器在打“3”点时的速度并填在表中.
②据(1)中表格,在图2中画出小车的速度时间图象.

①据上面记录,计算打点计时器在打“3”点时的速度并填在表中.
| 位置 | 1 | 2 | 3 | 4 | 5 |
| v/(m?s-1) | 1.2 | 1.0 | 0.6 | 0.4 |
10.质点从静止开始做匀加速直线运动,从开始运动起,通过连续三段位移所用的时间分别为1s、2s、3s,这三段位移之比应是( )
0 145754 145762 145768 145772 145778 145780 145784 145790 145792 145798 145804 145808 145810 145814 145820 145822 145828 145832 145834 145838 145840 145844 145846 145848 145849 145850 145852 145853 145854 145856 145858 145862 145864 145868 145870 145874 145880 145882 145888 145892 145894 145898 145904 145910 145912 145918 145922 145924 145930 145934 145940 145948 176998
| A. | 1:2:3 | B. | 1:3:5 | C. | 12:22:32 | D. | 1:23:33 |
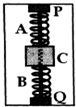 图示装置可以用来测量飞行器的加速度.矩形箱内上、下两壁上固定有可以测力的传感器P、Q,滑块C穿在矩形箱内一固定的光滑细杆上,且能自由滑动,两根完全相同的轻弹簧A、B-端固定在物体C上,另一端分别与传感器P、Q相连接.现将该装置固定在火箭上,火箭点火前,传感器P在上、Q在下且PQ连线在同一竖直线上,此时P、Q传给测控中心的示数均为1.0N.火箭点火后竖直向上加速飞到离地面距离为$\frac{R}{9}$的D处时(R是地球的半径),Q传回地面的示数为1.2N,取g=10m/s2,求:
图示装置可以用来测量飞行器的加速度.矩形箱内上、下两壁上固定有可以测力的传感器P、Q,滑块C穿在矩形箱内一固定的光滑细杆上,且能自由滑动,两根完全相同的轻弹簧A、B-端固定在物体C上,另一端分别与传感器P、Q相连接.现将该装置固定在火箭上,火箭点火前,传感器P在上、Q在下且PQ连线在同一竖直线上,此时P、Q传给测控中心的示数均为1.0N.火箭点火后竖直向上加速飞到离地面距离为$\frac{R}{9}$的D处时(R是地球的半径),Q传回地面的示数为1.2N,取g=10m/s2,求:

