5.一个静止的母核发生α衰变,产生的α粒子和子核的动能之和称为这个母核的α衰变能.
(1)若在一次α衰变中静止的母核放出的α粒子动能为E,又知α粒子质量为m,子核Y的质量为M,求母核的α衰变能.
(2)若母核释放的核能全部转化为α粒子和子核的动能,试分别判断${\;}_{28}^{44}$Cu和${\;}_{94}^{212}$Po能否发生α衰变?若能,求出其α衰变能(lu相当于931.5MeV,结果保留三位有效数字)
附:一些原子核的静止质量
(1)若在一次α衰变中静止的母核放出的α粒子动能为E,又知α粒子质量为m,子核Y的质量为M,求母核的α衰变能.
(2)若母核释放的核能全部转化为α粒子和子核的动能,试分别判断${\;}_{28}^{44}$Cu和${\;}_{94}^{212}$Po能否发生α衰变?若能,求出其α衰变能(lu相当于931.5MeV,结果保留三位有效数字)
附:一些原子核的静止质量
| 原子核 | 原子质量(u) |
| ${\;}_{2}^{4}$He | 4.0026 |
| ${\;}_{27}^{60}$Co | 59.9338 |
| ${\;}_{28}^{64}$Cu | 63.9298 |
| ${\;}_{92}^{208}$Pb | 207.9766 |
| ${\;}_{84}^{212}$Po | 211.9889 |
18. ${\;}_{92}^{238}Th$(钍核)的衰变方程为${\;}_{92}^{238}Th→{\;}_{93}^{238}pa+{\;}_{-1}^0e$,如图是剩余钍核的质量随时间变化关系的曲线,其中T为半衰期,则( )
${\;}_{92}^{238}Th$(钍核)的衰变方程为${\;}_{92}^{238}Th→{\;}_{93}^{238}pa+{\;}_{-1}^0e$,如图是剩余钍核的质量随时间变化关系的曲线,其中T为半衰期,则( )
 ${\;}_{92}^{238}Th$(钍核)的衰变方程为${\;}_{92}^{238}Th→{\;}_{93}^{238}pa+{\;}_{-1}^0e$,如图是剩余钍核的质量随时间变化关系的曲线,其中T为半衰期,则( )
${\;}_{92}^{238}Th$(钍核)的衰变方程为${\;}_{92}^{238}Th→{\;}_{93}^{238}pa+{\;}_{-1}^0e$,如图是剩余钍核的质量随时间变化关系的曲线,其中T为半衰期,则( )| A. | 该衰变的实质是核外电子摆脱原子核的束缚,发生逃逸 | |
| B. | 该衰变的实质是原子核内一个中子转化为一个质子和一个电子 | |
| C. | 图中k=3 | |
| D. | 图中k=4 |
17. 如图所示,静止在平板车C上的A、B两物块间有一根被压缩的弹簧,已知A物块质量大于B物块质量,A、B与平板车上表面间的动摩擦因数相同,地面光滑,当弹簧突然释放后,A、B两物块在平板车上滑动过程中,下列判断正确的是( )
如图所示,静止在平板车C上的A、B两物块间有一根被压缩的弹簧,已知A物块质量大于B物块质量,A、B与平板车上表面间的动摩擦因数相同,地面光滑,当弹簧突然释放后,A、B两物块在平板车上滑动过程中,下列判断正确的是( )
 如图所示,静止在平板车C上的A、B两物块间有一根被压缩的弹簧,已知A物块质量大于B物块质量,A、B与平板车上表面间的动摩擦因数相同,地面光滑,当弹簧突然释放后,A、B两物块在平板车上滑动过程中,下列判断正确的是( )
如图所示,静止在平板车C上的A、B两物块间有一根被压缩的弹簧,已知A物块质量大于B物块质量,A、B与平板车上表面间的动摩擦因数相同,地面光滑,当弹簧突然释放后,A、B两物块在平板车上滑动过程中,下列判断正确的是( )| A. | A、B系统动量守恒 | B. | A、B、C系统动量守恒 | ||
| C. | 平板车C向右运动 | D. | 平板车C向左运动 |
16. 如图所示,质量为m的小物块,在与水平方向成α角的力F作用下,沿光滑水平面运动,物块通过A点和B点的速度分别是vA和vB,物块由A运动到B的过程中( )
如图所示,质量为m的小物块,在与水平方向成α角的力F作用下,沿光滑水平面运动,物块通过A点和B点的速度分别是vA和vB,物块由A运动到B的过程中( )
0 145346 145354 145360 145364 145370 145372 145376 145382 145384 145390 145396 145400 145402 145406 145412 145414 145420 145424 145426 145430 145432 145436 145438 145440 145441 145442 145444 145445 145446 145448 145450 145454 145456 145460 145462 145466 145472 145474 145480 145484 145486 145490 145496 145502 145504 145510 145514 145516 145522 145526 145532 145540 176998
 如图所示,质量为m的小物块,在与水平方向成α角的力F作用下,沿光滑水平面运动,物块通过A点和B点的速度分别是vA和vB,物块由A运动到B的过程中( )
如图所示,质量为m的小物块,在与水平方向成α角的力F作用下,沿光滑水平面运动,物块通过A点和B点的速度分别是vA和vB,物块由A运动到B的过程中( )| A. | 物块重力的冲量为零 | |
| B. | 力F的冲量方向跟物块动量变化的方向相同 | |
| C. | 力F的冲量大小为mvB-mvA | |
| D. | 力F做的功为$\frac{1}{2}$mvB2-$\frac{1}{2}$mvA2 |
 如图,是一列简谐横波在t1时刻的波形图,质点P在该时刻的振动方向沿y轴负向,t2时刻质点P的振动速度与t1时刻的速度大小相等,方向相同;t3时刻质点P的速度与t1时刻的速度大小相等,方向相反,若t2-t1=t3-t2=0.2s,求这列波的传播速度.
如图,是一列简谐横波在t1时刻的波形图,质点P在该时刻的振动方向沿y轴负向,t2时刻质点P的振动速度与t1时刻的速度大小相等,方向相同;t3时刻质点P的速度与t1时刻的速度大小相等,方向相反,若t2-t1=t3-t2=0.2s,求这列波的传播速度. 如图所示,气缸呈圆柱形,上部有挡板,内部高度为h,筒内一个很薄的质量不计的活塞封闭一定量的理想气体,开始时活塞处于离底部$\frac{2}{3}$h的高度,外界大气压强为pc=1.0×105Pa,温度为27℃,现对气体加热,求:
如图所示,气缸呈圆柱形,上部有挡板,内部高度为h,筒内一个很薄的质量不计的活塞封闭一定量的理想气体,开始时活塞处于离底部$\frac{2}{3}$h的高度,外界大气压强为pc=1.0×105Pa,温度为27℃,现对气体加热,求: 一定质量的某种理想气体从状态A经状态B变化到状态C,该过程中气体体积V与热力学温度T的关系图象如图所示,图中线段AB与V轴平行,BC延长线过坐标原点O,又知气体在状态B时的压强pB=1.0×104Pa,从状态B变化到状态C过程中气体向外界放热70J,求:
一定质量的某种理想气体从状态A经状态B变化到状态C,该过程中气体体积V与热力学温度T的关系图象如图所示,图中线段AB与V轴平行,BC延长线过坐标原点O,又知气体在状态B时的压强pB=1.0×104Pa,从状态B变化到状态C过程中气体向外界放热70J,求: 在探究“外力的冲量与物体动量变化之间的关系”的实验中,一小组用如图所示实验装置进行定量探究,具体操作如下:先测出遮光片的宽度为d,钩码质量和小车(含遮光片)质量分别m、M,接着调整轨道倾角平衡小车受到的摩擦力,然后用小钩码通过细线拉动导轨上的小车在轨道上滑动,测得小车通过两光电门的遮光时间分别为t1、t2,在两光电门之间的运动时间为△t,已知重力加速度为g.
在探究“外力的冲量与物体动量变化之间的关系”的实验中,一小组用如图所示实验装置进行定量探究,具体操作如下:先测出遮光片的宽度为d,钩码质量和小车(含遮光片)质量分别m、M,接着调整轨道倾角平衡小车受到的摩擦力,然后用小钩码通过细线拉动导轨上的小车在轨道上滑动,测得小车通过两光电门的遮光时间分别为t1、t2,在两光电门之间的运动时间为△t,已知重力加速度为g.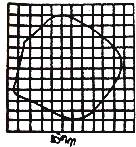 在“用油膜法估测分子大小”的实验中,油酸酒精溶液的浓度为每1000mL油酸酒精溶液中有油酸0.5mL,现用滴管向量筒内滴加50滴上述溶液,量筒中的溶液体积增加了1mL,若把一滴这样的油酸酒精溶液滴入足够大盛水的浅盘中,由于酒精溶于水,油酸在水面展开,稳定后形成的油膜形状如图所示,若每一小方格的边长为25mm,回答下列问题:
在“用油膜法估测分子大小”的实验中,油酸酒精溶液的浓度为每1000mL油酸酒精溶液中有油酸0.5mL,现用滴管向量筒内滴加50滴上述溶液,量筒中的溶液体积增加了1mL,若把一滴这样的油酸酒精溶液滴入足够大盛水的浅盘中,由于酒精溶于水,油酸在水面展开,稳定后形成的油膜形状如图所示,若每一小方格的边长为25mm,回答下列问题: