题目内容
5.一个静止的母核发生α衰变,产生的α粒子和子核的动能之和称为这个母核的α衰变能.(1)若在一次α衰变中静止的母核放出的α粒子动能为E,又知α粒子质量为m,子核Y的质量为M,求母核的α衰变能.
(2)若母核释放的核能全部转化为α粒子和子核的动能,试分别判断${\;}_{28}^{44}$Cu和${\;}_{94}^{212}$Po能否发生α衰变?若能,求出其α衰变能(lu相当于931.5MeV,结果保留三位有效数字)
附:一些原子核的静止质量
| 原子核 | 原子质量(u) |
| ${\;}_{2}^{4}$He | 4.0026 |
| ${\;}_{27}^{60}$Co | 59.9338 |
| ${\;}_{28}^{64}$Cu | 63.9298 |
| ${\;}_{92}^{208}$Pb | 207.9766 |
| ${\;}_{84}^{212}$Po | 211.9889 |
分析 原子核衰变过程中,动量守恒,由动量守恒定律得出子核Y与α粒子动量的关系,根据α粒子动能求出子核Y的动能.
衰变前后系统的动量守恒,根据质能方程△E=△mc2列式求解.
解答 解:(1)原子核衰变过程中,动量守恒,由动量守恒定律得
0=mv1-Mv2 ①又由动能表达式:E=$\frac{1}{2}$m${v}_{1}^{2}$ ②
子核的动能:EY=$\frac{1}{2}$M${v}_{2}^{2}$ ③
母核的α衰变能为E′=E+EY=(1+$\frac{m}{M}$)E
(2)若${\;}_{28}^{64}$Cu发生α衰变,方程为${\;}_{28}^{64}$Cu→${\;}_{27}^{60}$Co+${\;}_{2}^{4}$He
质量亏损△m=63.9298u-59.9338u-4.0026u=-0.0056u
质量增加,故${\;}_{28}^{64}$Cu不能发生α衰变.
若${\;}_{84}^{212}$Po发生α衰变,方程为${\;}_{84}^{212}$Po→${\;}_{92}^{208}$Pb+${\;}_{2}^{4}$He
质量亏损△m′=211.9889u-4.0026u-207.9766u=0.0097u
故${\;}_{84}^{212}$Po能发生α衰变,
由质能方程△E=△mc2
得${\;}_{84}^{212}$Po的α衰变为△E=0.0097×931.5MeV=9.04MeV.
答:(1)母核的α衰变能是(1+$\frac{m}{M}$)E
(2)${\;}_{84}^{212}$Po能发生α衰变,α衰变能是9.04MeV.
点评 应用动量守恒定律与质能方程即可正确解题,本题难度不大,是一道基础题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
13. 一列简谐波在t=0时刻的波形图如图中实线所示,从此刻起,经0.1s波形图如图中虚线所示,若波传播的速度为10m/s,则( )
一列简谐波在t=0时刻的波形图如图中实线所示,从此刻起,经0.1s波形图如图中虚线所示,若波传播的速度为10m/s,则( )
 一列简谐波在t=0时刻的波形图如图中实线所示,从此刻起,经0.1s波形图如图中虚线所示,若波传播的速度为10m/s,则( )
一列简谐波在t=0时刻的波形图如图中实线所示,从此刻起,经0.1s波形图如图中虚线所示,若波传播的速度为10m/s,则( )| A. | 这列波沿x轴正方向传播 | |
| B. | 这列波的周期T=0.4ns,其中n=1,2,3… | |
| C. | t=0时刻质点a沿y轴正方向运动 | |
| D. | 从t=0时刻起质点a经0.2通过的路程为0.4m |
10.假设两个相同的核A与B,质量均为2.0134u,动能均为E0,它们在不受其他力作用的情况下相向运动发生对心正碰,转变为C核与D粒子,且释放的核能△E全部转化为动能.设C核质量为3.0151u、动能为E1,D粒子质量为1.0087u、动能为E2,可以确定( )
| A. | 质量亏损为△m=0.0030u | B. | E1+E2=△E | ||
| C. | 释放核能△E=2E0 | D. | E1>E2 |
17.关于下列四幅图说法正确的是( )
| A. |  电子束通过铝箔时的衍射图样证实了电子具有粒子性 | |
| B. | 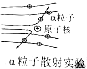 发现少数α粒子发生了较大偏转,说明原子的质量绝大部分集中在很小空间范围 | |
| C. |  根据玻尔理论,氢原子的轨道半径是任意的 | |
| D. |  光电效应实验说明光具有粒子性 |
14.真空中有两个静止的点电荷,它们之间的相互作用力大小为F.若它们的带电量都增大为原来的2倍,距离减小为原来的$\frac{1}{2}$,它们之间的相互作用力大小变为( )
| A. | $\frac{F}{4}$ | B. | F | C. | 4F | D. | 16F |
15.美国耶鲁大学的研究人员最近发现一颗新的星球,通过观测发现该星球的半径是地球的2倍,质量是地球的8倍,假设该星球有一颗近地卫星,则下列说法正确的是( )
| A. | 该星球的密度是地球密度的2倍 | |
| B. | 该星球表面的重力加速度是地球表面重力加速度的4倍 | |
| C. | 该星球的近地卫星的速度是地球近地卫速度的4倍 | |
| D. | 该星球的近地卫星周期跟地球的近地卫星周期相等 |
 a是静止在地球赤道上的物体,b是探测卫星,c是地球同步卫星,它们在同一平面内沿不同的轨道绕地心做匀速圆周运动,且均沿逆时针方向绕行,若某一时刻,它们正好运行到同一条直线上(如图甲所示).则再经过6小时,图中关于a、b和c三者位置的图示可能正确的是( )
a是静止在地球赤道上的物体,b是探测卫星,c是地球同步卫星,它们在同一平面内沿不同的轨道绕地心做匀速圆周运动,且均沿逆时针方向绕行,若某一时刻,它们正好运行到同一条直线上(如图甲所示).则再经过6小时,图中关于a、b和c三者位置的图示可能正确的是( )



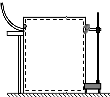 在“探究平抛运动的运动规律”的实验中,可以描绘出小球平抛运动的轨迹,实验简要步骤如下:
在“探究平抛运动的运动规律”的实验中,可以描绘出小球平抛运动的轨迹,实验简要步骤如下: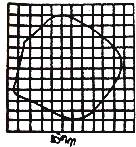 在“用油膜法估测分子大小”的实验中,油酸酒精溶液的浓度为每1000mL油酸酒精溶液中有油酸0.5mL,现用滴管向量筒内滴加50滴上述溶液,量筒中的溶液体积增加了1mL,若把一滴这样的油酸酒精溶液滴入足够大盛水的浅盘中,由于酒精溶于水,油酸在水面展开,稳定后形成的油膜形状如图所示,若每一小方格的边长为25mm,回答下列问题:
在“用油膜法估测分子大小”的实验中,油酸酒精溶液的浓度为每1000mL油酸酒精溶液中有油酸0.5mL,现用滴管向量筒内滴加50滴上述溶液,量筒中的溶液体积增加了1mL,若把一滴这样的油酸酒精溶液滴入足够大盛水的浅盘中,由于酒精溶于水,油酸在水面展开,稳定后形成的油膜形状如图所示,若每一小方格的边长为25mm,回答下列问题: