13.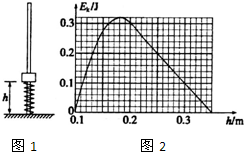 如图所示,竖直光滑杆固定不动,套在杆上的弹簧下端固定,将套在杆上的滑块向下压缩弹簧至离地面高度h=0.1m处,滑块与弹簧不拴接.现由静止释放滑块,通过传感器测量到滑块的速度和离地面高度h并作出滑块的动能Ek随高度h变化的图象,其中从0.2m上升到0.35m高度的范围内图象为直线,其余部分为曲线,以地面为零势能面,取g=10m/s2,由图象可知( )
如图所示,竖直光滑杆固定不动,套在杆上的弹簧下端固定,将套在杆上的滑块向下压缩弹簧至离地面高度h=0.1m处,滑块与弹簧不拴接.现由静止释放滑块,通过传感器测量到滑块的速度和离地面高度h并作出滑块的动能Ek随高度h变化的图象,其中从0.2m上升到0.35m高度的范围内图象为直线,其余部分为曲线,以地面为零势能面,取g=10m/s2,由图象可知( )
 如图所示,竖直光滑杆固定不动,套在杆上的弹簧下端固定,将套在杆上的滑块向下压缩弹簧至离地面高度h=0.1m处,滑块与弹簧不拴接.现由静止释放滑块,通过传感器测量到滑块的速度和离地面高度h并作出滑块的动能Ek随高度h变化的图象,其中从0.2m上升到0.35m高度的范围内图象为直线,其余部分为曲线,以地面为零势能面,取g=10m/s2,由图象可知( )
如图所示,竖直光滑杆固定不动,套在杆上的弹簧下端固定,将套在杆上的滑块向下压缩弹簧至离地面高度h=0.1m处,滑块与弹簧不拴接.现由静止释放滑块,通过传感器测量到滑块的速度和离地面高度h并作出滑块的动能Ek随高度h变化的图象,其中从0.2m上升到0.35m高度的范围内图象为直线,其余部分为曲线,以地面为零势能面,取g=10m/s2,由图象可知( )| A. | 小滑块的质量为0.1kg | |
| B. | 轻弹簧原长为0.2m | |
| C. | 弹簧的最大弹性势能为0.5J | |
| D. | 小滑块的重力势能与弹簧的弹性势能总和最小为0.4J |
12.下列表述符合物理学史实的是( )
| A. | 开普勒认为只有在一定的条件下,弹簧的弹力才与弹簧的形变量成正比 | |
| B. | 牛顿认为在足够高的山上以足够大的水平速度抛出物体,物体就不会再落到地球上 | |
| C. | 奥斯特发了电磁感应现象,并坚信电和磁之间存在一定的联系 | |
| D. | 安培首先引入电场线和磁感线,极大地促进了他对电磁现象的研究 |
11. 如图所示,在水平地面上的箱子内,用细线将质量均为m的两个球a、b分别系于箱子的上、下两底的内侧,轻质弹簧两端分别与球相连接,系统处于静止状态时,弹簧处于拉伸状态,下端细线对箱底的拉力为F,箱子的质量为M,则下列说法正确的是(重力加速度为g)( )
如图所示,在水平地面上的箱子内,用细线将质量均为m的两个球a、b分别系于箱子的上、下两底的内侧,轻质弹簧两端分别与球相连接,系统处于静止状态时,弹簧处于拉伸状态,下端细线对箱底的拉力为F,箱子的质量为M,则下列说法正确的是(重力加速度为g)( )
 如图所示,在水平地面上的箱子内,用细线将质量均为m的两个球a、b分别系于箱子的上、下两底的内侧,轻质弹簧两端分别与球相连接,系统处于静止状态时,弹簧处于拉伸状态,下端细线对箱底的拉力为F,箱子的质量为M,则下列说法正确的是(重力加速度为g)( )
如图所示,在水平地面上的箱子内,用细线将质量均为m的两个球a、b分别系于箱子的上、下两底的内侧,轻质弹簧两端分别与球相连接,系统处于静止状态时,弹簧处于拉伸状态,下端细线对箱底的拉力为F,箱子的质量为M,则下列说法正确的是(重力加速度为g)( )| A. | 系统处于静止状态时地面受到的压力大小为(M+2m)g-F | |
| B. | 系统处于静止状态时地面受到压力大小为(M+2m)g | |
| C. | 剪断连接球b与箱底的细线瞬间,地面受到的压力大小为(M+2m)g+F | |
| D. | 剪断连接球b与箱底的细线瞬间,地面受到的压力大小为(M+2m)g |
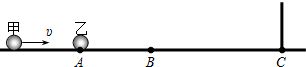
10.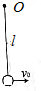 一质量不计的长为l的轻绳一端固定于O点,另一端系一质量为m的可视为质点的小球,开始小球静止于最低点,现给小球一水平向右的初速度,则下列说法正确的是( )
一质量不计的长为l的轻绳一端固定于O点,另一端系一质量为m的可视为质点的小球,开始小球静止于最低点,现给小球一水平向右的初速度,则下列说法正确的是( )
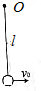 一质量不计的长为l的轻绳一端固定于O点,另一端系一质量为m的可视为质点的小球,开始小球静止于最低点,现给小球一水平向右的初速度,则下列说法正确的是( )
一质量不计的长为l的轻绳一端固定于O点,另一端系一质量为m的可视为质点的小球,开始小球静止于最低点,现给小球一水平向右的初速度,则下列说法正确的是( )| A. | 当小球在最低点的速度为$\sqrt{gl}$时,小球上升的最大高度小于$\frac{l}{2}$ | |
| B. | 当小球在最低点的速度为$\sqrt{3gl}$时,小球上升的最大高度等于$\frac{3l}{2}$ | |
| C. | 当小球在最低点的速度为$\sqrt{4gl}$时,小球上升的最大高度等于2l | |
| D. | 当小球在最低点的速度为$\sqrt{5gl}$时,小球上升的最大高度等于2l |
8.随着科技的发展,大量的科学实验促进了人们对微观领域的认识,下列说法正确的是( )
| A. | 玻尔建立了量子理论,成功解释了各种原子发光现象 | |
| B. | 德布罗意首先提出了物质波的猜想,而电子衍射实验证实了他的猜想 | |
| C. | 比结合能越大表示原子核中的核子结合得越牢固 | |
| D. | β衰变中产生的β射线是原子核外电子挣脱原子核束缚后形成的 | |
| E. | 一个处于n=4能级的氢原子向低能级跃迁时可能只放出三种不同频率的光子 |
5.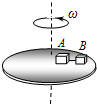 如图所示,在匀速转动的水平盘上,沿半径方向放着用细线相连的质量相等的两个物体A 和B(可视为质点),它们分居圆心同侧,与圆心距离分别为RA=r,RB=2r,与盘间的动摩擦因数μ相同,当圆盘转速缓慢加速到两物体刚好发生滑动的过程中,两物体与盘的最大静摩擦力等于滑动摩擦力,下列说法正确的是( )
如图所示,在匀速转动的水平盘上,沿半径方向放着用细线相连的质量相等的两个物体A 和B(可视为质点),它们分居圆心同侧,与圆心距离分别为RA=r,RB=2r,与盘间的动摩擦因数μ相同,当圆盘转速缓慢加速到两物体刚好发生滑动的过程中,两物体与盘的最大静摩擦力等于滑动摩擦力,下列说法正确的是( )
 如图所示,在匀速转动的水平盘上,沿半径方向放着用细线相连的质量相等的两个物体A 和B(可视为质点),它们分居圆心同侧,与圆心距离分别为RA=r,RB=2r,与盘间的动摩擦因数μ相同,当圆盘转速缓慢加速到两物体刚好发生滑动的过程中,两物体与盘的最大静摩擦力等于滑动摩擦力,下列说法正确的是( )
如图所示,在匀速转动的水平盘上,沿半径方向放着用细线相连的质量相等的两个物体A 和B(可视为质点),它们分居圆心同侧,与圆心距离分别为RA=r,RB=2r,与盘间的动摩擦因数μ相同,当圆盘转速缓慢加速到两物体刚好发生滑动的过程中,两物体与盘的最大静摩擦力等于滑动摩擦力,下列说法正确的是( )| A. | B物体所受到的摩擦力方向是先向左后向右 | |
| B. | 当ω<$\sqrt{\frac{μg}{2r}}$时,绳子的弹力为0 | |
| C. | 两物体刚好滑动时的角速度为ω=$\sqrt{\frac{2μg}{3r}}$ | |
| D. | 此时若烧断绳子,A仍相对盘静止,B将相对圆盘滑动 |
4. 我国首颗月球探测卫星“嫦娥一号”简化后的路线示意图如图所示.卫星由地面发射后,先经过地面发射轨道进入地球附近的停泊轨道做匀速圆周运动;然后从停泊轨道经过调控进入地月转移轨道;到达月球附近时,再次调控进入工作轨道做匀速圆周运动.这时卫星将开始对月球进行探测.已知地球与月球的质量之比为m,卫星的停泊轨道与工作轨道的轨道半径之比为n.则下列说法中正确的是( )
我国首颗月球探测卫星“嫦娥一号”简化后的路线示意图如图所示.卫星由地面发射后,先经过地面发射轨道进入地球附近的停泊轨道做匀速圆周运动;然后从停泊轨道经过调控进入地月转移轨道;到达月球附近时,再次调控进入工作轨道做匀速圆周运动.这时卫星将开始对月球进行探测.已知地球与月球的质量之比为m,卫星的停泊轨道与工作轨道的轨道半径之比为n.则下列说法中正确的是( )
0 143218 143226 143232 143236 143242 143244 143248 143254 143256 143262 143268 143272 143274 143278 143284 143286 143292 143296 143298 143302 143304 143308 143310 143312 143313 143314 143316 143317 143318 143320 143322 143326 143328 143332 143334 143338 143344 143346 143352 143356 143358 143362 143368 143374 143376 143382 143386 143388 143394 143398 143404 143412 176998
 我国首颗月球探测卫星“嫦娥一号”简化后的路线示意图如图所示.卫星由地面发射后,先经过地面发射轨道进入地球附近的停泊轨道做匀速圆周运动;然后从停泊轨道经过调控进入地月转移轨道;到达月球附近时,再次调控进入工作轨道做匀速圆周运动.这时卫星将开始对月球进行探测.已知地球与月球的质量之比为m,卫星的停泊轨道与工作轨道的轨道半径之比为n.则下列说法中正确的是( )
我国首颗月球探测卫星“嫦娥一号”简化后的路线示意图如图所示.卫星由地面发射后,先经过地面发射轨道进入地球附近的停泊轨道做匀速圆周运动;然后从停泊轨道经过调控进入地月转移轨道;到达月球附近时,再次调控进入工作轨道做匀速圆周运动.这时卫星将开始对月球进行探测.已知地球与月球的质量之比为m,卫星的停泊轨道与工作轨道的轨道半径之比为n.则下列说法中正确的是( )| A. | 卫星在停泊轨道和工作轨道运行的速度之比为$\frac{{\sqrt{n}}}{{\sqrt{m}}}$ | |
| B. | 卫星在停泊轨道和工作轨道运行的周期之比为$\frac{{n\sqrt{n}}}{{\sqrt{m}}}$ | |
| C. | 卫星在停泊轨道运行的速度小于地球的第一宇宙速度 | |
| D. | 卫星从停泊轨道到进入工作轨道的过程中卫星机械能守恒 |
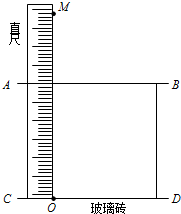 现要估测一矩形玻璃砖的折射率n,给定的器材有:待测玻璃砖、白纸、铅笔、大头针1枚、直尺、直角三角板.实验时,先将直尺的一端O和另一点M标上两个明显的标记,再将玻璃砖平放在白纸上,沿其两个长边在白纸上画出两条直线AB、CD,再将直尺正面紧贴玻璃砖的左边缘放置,使O点与直线CD相交,并在白纸上记下点O、点M的位置,如图所示,然后在右上方通过AB所在界面向左下方观察,调整视线方向,直到O点的像与M点的像重合,再在AB直线上插上大头针,使大头针挡住M、O的像,记下大头针P点的位置.
现要估测一矩形玻璃砖的折射率n,给定的器材有:待测玻璃砖、白纸、铅笔、大头针1枚、直尺、直角三角板.实验时,先将直尺的一端O和另一点M标上两个明显的标记,再将玻璃砖平放在白纸上,沿其两个长边在白纸上画出两条直线AB、CD,再将直尺正面紧贴玻璃砖的左边缘放置,使O点与直线CD相交,并在白纸上记下点O、点M的位置,如图所示,然后在右上方通过AB所在界面向左下方观察,调整视线方向,直到O点的像与M点的像重合,再在AB直线上插上大头针,使大头针挡住M、O的像,记下大头针P点的位置.