题目内容
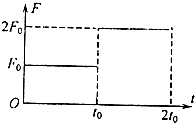
如图所示,装置的左边是足够长的光滑水平台面,一轻质弹簧左端固定,右端连接着质量M=1kg的小物块A,装置的中间是水平传送带,它与左、右两边的台面等高,并能平滑对接.传送带始终以v=1m/s的速率逆时针转动.装置的右边是一光滑曲面,质量m=0.5kg的小物块B从其上距水平台面高h=0.8m处由静止释放.已知物块B与传送带之间的动摩擦因数μ=0.35,l=1.0m.设物块A、B间发生的是对心弹性碰撞,第一次碰撞前物块A处于静止状态.取g=10m/s2.
(1)求物块B与物块A第一次碰撞前的速度大小.
(2)通过计算说明物块B与物块A第一次碰撞后能否运动到右边的曲面上?
(3)如果物块A,B每次碰撞后,弹簧恢复原长时都会立即被锁定,而当它们再次碰撞前锁定被解除,试求出物块B第n次碰撞后的运动速度大小.

(1)求物块B与物块A第一次碰撞前的速度大小.
(2)通过计算说明物块B与物块A第一次碰撞后能否运动到右边的曲面上?
(3)如果物块A,B每次碰撞后,弹簧恢复原长时都会立即被锁定,而当它们再次碰撞前锁定被解除,试求出物块B第n次碰撞后的运动速度大小.

(1)设物块B沿光滑曲面下滑到水平位置时的速度大小为v0,由机械能守恒定律可得:
mgh=
mv02,
解得:v0=
=
=4m/s,
设物块B在传送带上滑动过程中因受摩擦力所产生的加速度大小为a,则有:μmg=ma,
设物块B通过传送带后运动速度大小为v,有:v12-v02=-2al,
解得:v1=3m/s>v=1m/s,则物块B与物块A第一次碰撞前的速度大小为3m/s;
(2)设物块A、B第一次碰撞后的速度分别为vA、vB,取向右为正方向,由动量守恒定律得:
-mv1=MvA+mvB,
由机械能守恒定律得:
mv2=
mvB2+
MvA2,
解得:vA=-2m/s,vB=1m/s,(vA=0m/s,vB=-3m/s不符合题意,舍去)
即碰撞后物块B在水平台面向右匀速运动,设物块B在传送带上向右运动的最大位移为l',则有:
0-vB2=-2al′,
解得:l′=
<l,
所以物块B不能通过传送带运动到右边的曲面上;
(3)当物块B在传送带上向右运动的速度为零时,将会沿传送带向左加速.可以判断,物块B运动到左边台面是的速度大小为vB,继而与物块A发生第二次碰撞.
由(2)可知,vB=
v1,
同理可得:第二次碰撞后B的速度:vB1=
vB=(
)2v1,
…
第n次碰撞后B的速度为:vB(n-1)=(
)nv1=(
)n×3=)=(
)n-1m/s;
答:(1)物块B与物块A第一次碰撞前的速度大小为3m/s.
(2)物块B与物块A第一次碰撞不能运动到右边的曲面上;
(3)物块B第n次碰撞后的运动速度大小为(
)n-1m/s.
mgh=
| 1 |
| 2 |
解得:v0=
| 2gh |
| 2×10×0.8 |
设物块B在传送带上滑动过程中因受摩擦力所产生的加速度大小为a,则有:μmg=ma,
设物块B通过传送带后运动速度大小为v,有:v12-v02=-2al,
解得:v1=3m/s>v=1m/s,则物块B与物块A第一次碰撞前的速度大小为3m/s;
(2)设物块A、B第一次碰撞后的速度分别为vA、vB,取向右为正方向,由动量守恒定律得:
-mv1=MvA+mvB,
由机械能守恒定律得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:vA=-2m/s,vB=1m/s,(vA=0m/s,vB=-3m/s不符合题意,舍去)
即碰撞后物块B在水平台面向右匀速运动,设物块B在传送带上向右运动的最大位移为l',则有:
0-vB2=-2al′,
解得:l′=
| 1 |
| 7 |
所以物块B不能通过传送带运动到右边的曲面上;
(3)当物块B在传送带上向右运动的速度为零时,将会沿传送带向左加速.可以判断,物块B运动到左边台面是的速度大小为vB,继而与物块A发生第二次碰撞.
由(2)可知,vB=
| 1 |
| 3 |
同理可得:第二次碰撞后B的速度:vB1=
| 1 |
| 3 |
| 1 |
| 3 |
…
第n次碰撞后B的速度为:vB(n-1)=(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
答:(1)物块B与物块A第一次碰撞前的速度大小为3m/s.
(2)物块B与物块A第一次碰撞不能运动到右边的曲面上;
(3)物块B第n次碰撞后的运动速度大小为(
| 1 |
| 3 |

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目

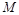 的小车,车上表面水平且光滑,车上装有半径为
的小车,车上表面水平且光滑,车上装有半径为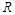 的光滑四分之一圆环轨道,圆环轨道质量不计且与车的上表面相切,质量为
的光滑四分之一圆环轨道,圆环轨道质量不计且与车的上表面相切,质量为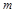 的小滑块从跟车面等高的平台以
的小滑块从跟车面等高的平台以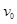 的初速度滑上小车(
的初速度滑上小车(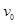 足够大,以至滑块能够滑过与环心O等高的b点),试求:
足够大,以至滑块能够滑过与环心O等高的b点),试求: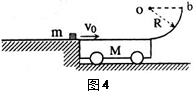 (2)滑块从滑上小车至滑到环心O等高的b点过程中,车的上表面和环的弹力共对滑块做了多少功?
(2)滑块从滑上小车至滑到环心O等高的b点过程中,车的上表面和环的弹力共对滑块做了多少功?