题目内容
 如图所示,在MN左侧有相距为d的两块正对的平行金属板P、Q,板长L=
如图所示,在MN左侧有相距为d的两块正对的平行金属板P、Q,板长L=| 3 |
(1)粒子从下极板边缘射出时的速度;
(2)粒子从O运动到A经历的时间;
(3)矩形有界磁场的最小面积.
分析:(1)带电粒子做平抛运动,由运动的分解可得平行极板方向做匀速运动,垂直此方向做匀加速运动,根据运动学公式即可求解;
(2)粒子做平抛运动后进入磁场做匀速圆周运动,根据几何关系可得已知长度与运动轨迹的半径的表达式.再由轨迹对应的圆心角,从而求出所需要的时间;
(3)从几何角度得出磁场的最小区域,再由面积公式即可求解.
(2)粒子做平抛运动后进入磁场做匀速圆周运动,根据几何关系可得已知长度与运动轨迹的半径的表达式.再由轨迹对应的圆心角,从而求出所需要的时间;
(3)从几何角度得出磁场的最小区域,再由面积公式即可求解.
解答: 解:(1)带电粒子在电场中平行极板方向匀速运动:
解:(1)带电粒子在电场中平行极板方向匀速运动:
d=v0t
竖直方向从静止开始做匀加速运动:
d=
vyt,
解得vy=
v0
则粒子从下极板边缘射出时的速度为v=
=2v0,
且与竖直方向成300角.
(2)带电粒子在电场中运动的时间t1=
d,由几何关系可得r=
,
离开电场后先做匀速运动,匀速运动的时间t2=
r=
d
然后进入磁场,在磁场中偏转1200到达A,
t3=
=
=
所以带电粒子从O运动至A所用的总时间为
t=t1+t2+t3=(
+
)
(3)由轨迹示意图可知,磁场区域宽等于轨迹半径r,高等于
,而r=
,
所以矩形有界磁场的最小面积为S=r×
=
答:(1)粒子从下极板边缘射出时的速度为2v0,方向与竖直方向成300角;
(2)粒子从O运动到A经历的时间时间=(
+
)
;
(3)矩形有界磁场的最小面积为
.
 解:(1)带电粒子在电场中平行极板方向匀速运动:
解:(1)带电粒子在电场中平行极板方向匀速运动:
| ||
| 3 |
竖直方向从静止开始做匀加速运动:
| 1 |
| 2 |
| 1 |
| 2 |
解得vy=
| 3 |
则粒子从下极板边缘射出时的速度为v=
|
且与竖直方向成300角.
(2)带电粒子在电场中运动的时间t1=
| ||
| 3v0 |
| d |
| 3 |
离开电场后先做匀速运动,匀速运动的时间t2=
| ||
| 2v0 |
| ||
| 6v0 |
然后进入磁场,在磁场中偏转1200到达A,
t3=
| T |
| 3 |
| 2πr |
| 6v0 |
| πd |
| 9v0 |
所以带电粒子从O运动至A所用的总时间为
t=t1+t2+t3=(
| ||
| 2 |
| π |
| 9 |
| d |
| v0 |
(3)由轨迹示意图可知,磁场区域宽等于轨迹半径r,高等于
| 3r |
| 2 |
| d |
| 3 |
所以矩形有界磁场的最小面积为S=r×
| 3r |
| 2 |
| d2 |
| 6 |
答:(1)粒子从下极板边缘射出时的速度为2v0,方向与竖直方向成300角;
(2)粒子从O运动到A经历的时间时间=(
| ||
| 2 |
| π |
| 9 |
| d |
| v0 |
(3)矩形有界磁场的最小面积为
| d2 |
| 6 |
点评:理解平抛运动处理的运动分解规律,掌握匀速圆周运动的:定圆心、画轨迹、求半径的方法.同时运用几何知识来结合求解.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 的两块正对的平行金属板P、Q,板长
的两块正对的平行金属板P、Q,板长 两板带等量异种电荷,上极板带负电。在MN右侧存在垂直于纸面的矩形匀强磁场(图中未画出),其左边界和下边界分别与MN、AA’重合(边界上有磁场)。现有一带电粒子以初速度v0沿两板中央OO′射入,并恰好从下极板边缘射出,又经过在矩形有界磁场中的偏转,最终垂直于MN从A点向左水平射出。 已知A点与下极板右端的距离为d。不计带电粒子重力。求:
两板带等量异种电荷,上极板带负电。在MN右侧存在垂直于纸面的矩形匀强磁场(图中未画出),其左边界和下边界分别与MN、AA’重合(边界上有磁场)。现有一带电粒子以初速度v0沿两板中央OO′射入,并恰好从下极板边缘射出,又经过在矩形有界磁场中的偏转,最终垂直于MN从A点向左水平射出。 已知A点与下极板右端的距离为d。不计带电粒子重力。求: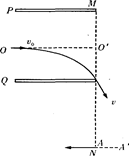
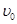 自O点沿水平方向射入,并恰好从P点射出,又经过在矩形有界磁场中的偏转,最终垂直于MN从A点向左水平射出。已知PA距离为d,
自O点沿水平方向射入,并恰好从P点射出,又经过在矩形有界磁场中的偏转,最终垂直于MN从A点向左水平射出。已知PA距离为d,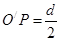 ,
, 距离
距离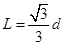 。不计带电粒子重力。
。不计带电粒子重力。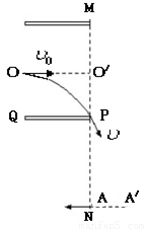
 的两块正对的平行金属板P、Q,板长
的两块正对的平行金属板P、Q,板长 两板带等量异种电荷,上极板带负电。在MN右侧存在垂直于纸面的矩形匀强磁场(图中未画出),其左边界和下边界分别与MN、AA’重合(边界上有磁场)。现有一带电粒子以初速度v0沿两板中央OO′射入,并恰好从下极板边缘射出,又经过在矩形有界磁场中的偏转,最终垂直于MN从A点向左水平射出。 已知A点与下极板右端的距离为d。不计带电粒子重力。求:
两板带等量异种电荷,上极板带负电。在MN右侧存在垂直于纸面的矩形匀强磁场(图中未画出),其左边界和下边界分别与MN、AA’重合(边界上有磁场)。现有一带电粒子以初速度v0沿两板中央OO′射入,并恰好从下极板边缘射出,又经过在矩形有界磁场中的偏转,最终垂直于MN从A点向左水平射出。 已知A点与下极板右端的距离为d。不计带电粒子重力。求: