题目内容
（8分）如图所示，在倾角为θ的斜面上，一物块（可视为质点）通过轻绳牵拉压紧弹簧．现将轻绳烧断，物块被弹出，与弹簧分离后即进入足够长的N N /粗糙斜面（虚线下方的摩擦不计），沿斜面上滑达到最远点位置离N距离为S．此后下滑，第一次回到N处，压缩弹簧后又被弹离，第二次上滑最远位置离N距离为S/2．求：物块与粗糙斜面间N N /段的动摩擦因数
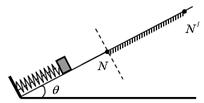
μ="1/3" tgθ
第一次下滑回到N时速度为v
Mgsinθ·S－μmgcosθ·S=mv2/2 ① （3分）
第二次上滑,初速度也为v
mgsinθ·S/2+μmgcosθ·S/2= mv2/2 ② （3分）
联立方程①、②，解得μ="1/3" tgθ （2分）
（或直接对动能为零的两个状态及过程运用动能定理：
mgsinθ·S/2 –μmgcosθ·3S/2 =" 0 " 解得μ="1/3" tgθ同样给分）
Mgsinθ·S－μmgcosθ·S=mv2/2 ① （3分）
第二次上滑,初速度也为v
mgsinθ·S/2+μmgcosθ·S/2= mv2/2 ② （3分）
联立方程①、②，解得μ="1/3" tgθ （2分）
（或直接对动能为零的两个状态及过程运用动能定理：
mgsinθ·S/2 –μmgcosθ·3S/2 =" 0 " 解得μ="1/3" tgθ同样给分）
练习册系列答案
相关题目
kg、长度L="2.0m." 铁块A静止于木板的右端，其质量
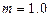kg，与木板间的动摩擦因数
，并可看作质点。现给木板B施加一个水平向右的恒定拉力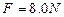
，使木板从铁块下方抽出，试求：（取g=10m/s2）
）
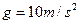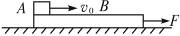
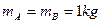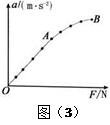
，A、B间动摩擦因数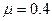
，现对物体A施加一水平力F，F-t关系图像如图所示。两物体在力F作用下由静止开始运动，且B物体足够长。若向右为正方向，则对物体的运动，下列说法正确的是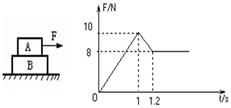
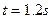时，A物体速度达到最大
50 N和70 N，它们与水平地面之间的动摩擦因数均为0.2，与A、B相连接的轻弹簧被压缩了5 cm，系统置于水平地
面上静止不动。已知弹簧的劲度系数为100 N/m。用F
=7N的水平力作用在木块A上，如图所示，力F作用后( )