题目内容
7．关于位移和路程，下列说法正确的是（ ）| A． | 位移就是路程 | |
| B． | 物体通过的路程不等，但位移可能相等 | |
| C． | 位移的大小永远不等于路程 | |
| D． | 物体通过一段路程，但位移不可能为零 |
分析 位移是矢量，位移的方向由初位置指向末位置．位移的大小不大于路程．路程是标量，是运动路径的长度．当质点做单向直线运动时，位移的大小一定等于路程．
解答 解：A、路程没有方向，只有大小，是标量，位移是矢量，位移的方向由初位置指向末位置，路程是标量，是运动路径的长度，不能说位移就是路程；故A错误
B、物体通过的路程不等，但位移可以相等，故B正确
C、当质点做单向直线运动时，位移的大小一定等于路程．故C错误
D、物体通过一段路程，若回到出发点，位移为零，故D错误
故选：B．
点评 考查位移与路程的区别与联系，位移与路程是描述运动常用的物理量，它们之间大小关系是位移大小≤路程．
练习册系列答案
阅读快车系列答案
相关题目
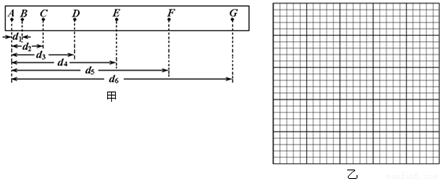
17．在“研究小车的匀加速直线”运动的实验时，某同学得到一条用打点计时器打下的纸带如图甲所示，并在其上取了A、B、C、D、E、F、G等7个计数点，每相邻两个计数点间还有4个点，图中没有画出，打点计时器接周期为T=0.02s的交流电源．他经过测量并计算得到打点计时器在打B、C、D、E、F各点时小车的瞬时速度如下表：
（1）纸带的左（填“左”或“右”）端与小车相连；
（2）计算在打F点时小车瞬时速度的表达式为vF=$\frac{{d}_{6}-{d}_{4}}{10T}$；
（3）根据（1）中得到的数据，以A点对应的时刻计为t=0，试在图乙中所给的坐标系中，作出v-t图象；
（4）根据上题中v-t图线，求小车运动的加速度a=0.43 m/s2；
| 对应点 | 速度（m/s） |
| B | 0.122 |
| C | 0.164 |
| D | 0.205 |
| E | 0.250 |
| F | 0.289 |
（2）计算在打F点时小车瞬时速度的表达式为vF=$\frac{{d}_{6}-{d}_{4}}{10T}$；
（3）根据（1）中得到的数据，以A点对应的时刻计为t=0，试在图乙中所给的坐标系中，作出v-t图象；
（4）根据上题中v-t图线，求小车运动的加速度a=0.43 m/s2；
18．
如图所示，在粗糙水平板上放一个物体，使水平板和物体一起在竖直平 面内沿逆时针方向做匀速圆周运动，ab为水平直径，cd为竖直直径，在运动过程中木板始终保持水平，物块相对木板始终静止，则（ ）
如图所示，在粗糙水平板上放一个物体，使水平板和物体一起在竖直平 面内沿逆时针方向做匀速圆周运动，ab为水平直径，cd为竖直直径，在运动过程中木板始终保持水平，物块相对木板始终静止，则（ ）| A． | 物块始终受到三个力作用 | |
| B． | 只有在a、b、c、d四点，物块受到合外力才指向圆心 | |
| C． | 从a到b，物体所受的摩擦力先减小后增大 | |
| D． | 从b到a，物块处于失重状态 |
15．下列关于摩擦力的说法正确的是（ ）
| A． | 摩擦力的大小一定与正压力成正比 | |
| B． | 摩擦力的方向总和物体的运动方向或运动趋势方向相反 | |
| C． | 受滑动摩擦力作用物体一定是运动的 | |
| D． | 有摩擦力则一定有弹力，且摩擦力与对应的弹力方向一定互相垂直 |
在“验证力的平行四边形定则”实验中，需要将橡皮条的一端固定在水平木板上，另一端系上两根细绳，细绳的另一端都有绳套（如图）．
有一个物体做直线运动，其速度--时间图象如图所示，从图中判断0-2s，2-4s，4-6s，6-8s各阶段的运动情况．
19．
如图所示，N=10匝、边长L=1m的正方形线圈绕与匀强磁场垂直的中心轴OO′沿逆时针方向转动，转速n=120r/min，磁感应强度B=$\frac{2}{π}$ T，引出线的两端分别与相互绝缘的两个半圆形铜环相连．两个半圆形铜环又通过固定的电刷M和N与电阻R相连．线圈从图中位置开始转动过程中，（ ）
如图所示，N=10匝、边长L=1m的正方形线圈绕与匀强磁场垂直的中心轴OO′沿逆时针方向转动，转速n=120r/min，磁感应强度B=$\frac{2}{π}$ T，引出线的两端分别与相互绝缘的两个半圆形铜环相连．两个半圆形铜环又通过固定的电刷M和N与电阻R相连．线圈从图中位置开始转动过程中，（ ）| A． | 线圈从图中位置转动180°的过程中，通过电阻R的电荷量为零 | |
| B． | t=$\frac{1}{12}$s时，线圈与中性面所成夹角是60° | |
| C． | 流过R的电流大小不断变化，方向总是M→R→N | |
| D． | 若将电阻R换成耐压值为82V的电容器，电容器不会被击穿 |
16．以v0的速度水平抛出一物体，当其水平分位移与竖直分位移相等时，下列说法正确的是（ ）
| A． | 运动的位移是$\frac{2\sqrt{2}{v}_{0}}{g}$ | |
| B． | 竖直分速度的大小等于水平分速度的大小 | |
| C． | 运动的时间是$\frac{2{v}_{0}}{g}$ | |
| D． | 即时速度的大小是2v0 |