题目内容
17. 如图所示,倾角为α的光滑固定斜面,斜面上相隔为d的平行虚线MN与PQ间有大小为B的匀强磁场,方向垂直斜面向下.一质量为m,电阻为R,边长为L的度v匀速进入磁场,线圈ab边刚进入磁场和cd边刚要离开磁场时,ab边两端的电压相等.已知磁场的宽度d大于线圈的边长L,重力加速度为g.求
如图所示,倾角为α的光滑固定斜面,斜面上相隔为d的平行虚线MN与PQ间有大小为B的匀强磁场,方向垂直斜面向下.一质量为m,电阻为R,边长为L的度v匀速进入磁场,线圈ab边刚进入磁场和cd边刚要离开磁场时,ab边两端的电压相等.已知磁场的宽度d大于线圈的边长L,重力加速度为g.求(1)线圈进入磁场的过程中,通过ab边的电量q;
(2)恒力F的大小;
(3)线圈通过磁场的过程中,ab边产生的热量Q.
分析 (1)根据电量公式、欧姆定律和法拉第电磁感应定律结合求解电量.
(2)线圈匀速进入磁场,受力平衡,根据平衡条件和安培力公式求解.
(3)根据法拉第电磁感应定律和闭合电路欧姆定律结合得到线圈ab边刚进入磁场和cd边刚要离开磁场时,ab间的电压与速度的关系,从而求得cd边刚要离开磁场时的速度,再由动能定理和功能关系求解热量.
解答 解:(1)线圈进入磁场过程中,通过线框横截面的电量 $q=\overline I△t$ ①
根据欧姆定律有 $\overline I=\frac{\overline E}{R}$ ②
根据法拉第电磁感应定律 $\overline E=N\frac{△ϕ}{△t}$ ③
线框进入磁场过程中的磁通量变化△ϕ=BL2 ④
由①②③④式解得 $q=\frac{{B{L^2}}}{R}$ ⑤
(2)线圈匀速进入磁场,根据平衡有 F=mgsinα+F安 ⑥
线圈受到的安培力 F安=BIL ⑦
根据欧姆定律 $I=\frac{E}{R}$ ⑧
根据法拉第定磁感应定律 E=BLv ⑨
由⑥⑦⑧⑨式解得 $F=mgsinα+\frac{{{B^2}{L^2}v}}{R}$ ⑩
(3)线圈ab边刚进入磁场时,根据法拉第电磁感应定律和闭合电路欧姆定律 ${U_{ab}}=\frac{3}{4}BLv$⑪
线圈cd边刚要离开磁场时,根据法拉第电磁感应定律和闭合电路欧姆定律 ${U_{ab}}=\frac{1}{4}BL{v_1}$⑫
线圈通过磁场的过程中,根据动能定理有 $F(L+d)-mg(L+d)sinα-{W_安}=\frac{1}{2}mv_1^2-\frac{1}{2}m{v^2}$⑬
根据安培力做功和电热的关系有 W安=Q总⑭
根据热量分配关系有 $Q=\frac{1}{4}{Q_总}$⑮
由⑩⑪⑫⑬⑭⑮式解得$Q=\frac{{{B^2}{L^2}v(L+d)}}{4R}-m{v^2}$⑯
答:
(1)线圈进入磁场的过程中,通过ab边的电量q为$\frac{B{L}^{2}}{R}$;
(2)恒力F的大小为mgsinα+$\frac{{B}^{2}{L}^{2}v}{R}$;
(3)线圈通过磁场的过程中,ab边产生的热量Q为$\frac{{B}^{2}{L}^{2}v(L+d)}{4R}$-mv2.
点评 本题中感应电荷量的结论可在会推导的基础上记牢,经常用到.分析清楚线圈的运动过程是正确解题的关键,解题时要注意:E=BLv、欧姆定律、安培力公式、平衡条件、动能定理与能量守恒定律的应用,求热量时,要注意线框进入和穿出磁场两个过程都要产生焦耳热.

 阅读快车系列答案
阅读快车系列答案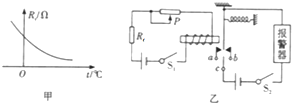
| A. | 为了使温度过高时报警器响铃,c应接在a处 | |
| B. | 为了使温度过高时报警器响铃,c应接在b处 | |
| C. | 若使启动报警的温度提高些,则应将滑动变阻器滑片P向左移动 | |
| D. | 如果在调试报警器达最低报警温度时,无论如何调节滑片P都不能报警,且电路无故障,可能原因是左边电源电压太低 |
| A. | A、B两球的运动方向相同 | B. | A、B两球的运动方向相反 | ||
| C. | A球静止 | D. | B球静止 |
| A. | 速度是表示物体运动快慢的物理量,既有大小,又有方向,是矢量 | |
| B. | 平均速度就是速度的平均值,它只有大小,没有方向,是标量 | |
| C. | 运动物体在某一时刻或某一位置的速度,叫做瞬时速度,它是矢量 | |
| D. | 汽车上的速度计是用来测量汽车平均速度大小的仪器 |
 如图,导线ab、cd跨接在电阻不计,足够长光滑的导轨上,ab的电阻为2R,cd电阻为R,整个装置放置于匀强磁场中.当cd在外力F1作用下,匀速向右运动时,ab在外力F2的作用下保持静止.则F1、F2及两导线的端电压Uab、Ucd的关系为( )
如图,导线ab、cd跨接在电阻不计,足够长光滑的导轨上,ab的电阻为2R,cd电阻为R,整个装置放置于匀强磁场中.当cd在外力F1作用下,匀速向右运动时,ab在外力F2的作用下保持静止.则F1、F2及两导线的端电压Uab、Ucd的关系为( )| A. | F1>F2 | B. | F1=F2 | C. | Uab>Ucd | D. | Uab<Ucd |

 某兴趣小组准备探究“合外力做功和物体速度变化的关系”,实验前组员们提出了以下几种猜想:
某兴趣小组准备探究“合外力做功和物体速度变化的关系”,实验前组员们提出了以下几种猜想: 如图所示,线圈面积为0.05m2,共100匝,线圈总电阻为1Ω,与外电阻R=9Ω相连.当线圈在B=$\frac{2}{π}$T的匀强磁场中绕OO′以转速n=300r/min匀速转动时,求:
如图所示,线圈面积为0.05m2,共100匝,线圈总电阻为1Ω,与外电阻R=9Ω相连.当线圈在B=$\frac{2}{π}$T的匀强磁场中绕OO′以转速n=300r/min匀速转动时,求: