题目内容
9. 如图所示,线圈面积为0.05m2,共100匝,线圈总电阻为1Ω,与外电阻R=9Ω相连.当线圈在B=$\frac{2}{π}$T的匀强磁场中绕OO′以转速n=300r/min匀速转动时,求:
如图所示,线圈面积为0.05m2,共100匝,线圈总电阻为1Ω,与外电阻R=9Ω相连.当线圈在B=$\frac{2}{π}$T的匀强磁场中绕OO′以转速n=300r/min匀速转动时,求:(1)若从线圈处于中性面开始计时,写出电动势的瞬时值表达式;
(2)两电表A、V的示数;
(3)线圈转过$\frac{1}{60}$s时,电动势的瞬时值;
(4)线圈转过$\frac{1}{30}$s的过程中,通过电阻R的电荷量;
(5)线圈匀速转一周外力做的功.
分析 (1)从线圈处于中性面开始计时,电动势的瞬时值表达式为e=Emsinωt.感应电动势的最大值Em=nBSω,由题已知条件代入求出.
(2)交流电表测量有效值,由感应电动势的最大值,求出感应动势有效值,由欧姆定律求解两电表的读数.
(3)将时间代入 瞬时表达式即可得线圈转过$\frac{1}{60}$s时,电动势的瞬时值;
(4)由q=n$\frac{△Φ}{R+r}$可求解通过电阻的电荷量.
(4)根据焦耳定律Q=I2Rt求解线圈匀速转一圈产生的总热量,I为电流的有效值.
解答 解:
(1)线圈的角速度ω=2πn=10πrad/s,感应电动势的最大值Em=nBSω=100V,则从线圈处于中性面开始计时,电动势的瞬时值表达式为e=Emsinωt=100sin 10πtV
(2)电路中电流的有效值I=$\frac{E}{R+r}$,E=$\frac{\sqrt{2}}{2}$Em,代入解得I=5$\sqrt{2}$A,即电流表读数为5$\sqrt{2}$A.
电压表读数为U=IR=45$\sqrt{2}$V
(3)当线圈转过$\frac{1}{60}$ s时,电动势的瞬时值e=100sin(10π×$\frac{1}{60}$) V=50 V.
(4)线圈转过t=$\frac{1}{30}$ s的过程中,线圈转过的角度为:
θ=ωt=2πnt=2π×$\frac{300}{60}$×$\frac{1}{30}$=$\frac{π}{3}$
则通过电阻R的电荷量为q=It=$\frac{N△Φ}{△t(R+r)}×△t$=$\frac{N△Φ}{R+r}$=$\frac{1}{2π}$ C.
(5)线圈匀速转一圈产生的总热量Q=I2(R+r)T=I2R$•\frac{2π}{ω}$=(5$\sqrt{2}$)2×10×$\frac{2π}{10π}$=100 J.
答:
(1)若从线圈处于中性面开始计时,电动势的瞬时值表达式为100sin10πtV;
(2)电流表读数为5$\sqrt{2}$A,电压表读数为45$\sqrt{2}$V.
(3)当线圈转过$\frac{1}{60}$ s时,电动势的瞬时值为50V;
(4)线圈转过过$\frac{1}{30}$s的过程中,通过电阻的电荷量是$\frac{1}{2π}$ C.
(5)线圈匀速转一圈外力做的功为100J.
点评 本题考查交变电流规律的基本应用,注意交流电表测量的是交流电的有效值.并能正确根据功能关系分析能量的转化关系.

 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案 甲、乙两车在一平直公路上沿同一方向沿直线运动,已知t=0时刻乙车在甲车前面50m,它们的v-t图象如图所示.下列判断正确的是( )
甲、乙两车在一平直公路上沿同一方向沿直线运动,已知t=0时刻乙车在甲车前面50m,它们的v-t图象如图所示.下列判断正确的是( )| A. | 乙车启动时,甲车在其前方50m处 | |
| B. | 运动过程中,乙车落后甲车的最大距离为25m | |
| C. | 乙车启动10s后正好追上甲车 | |
| D. | 乙车超过甲车后,两车还会再相遇 |
| A. | 加速度和线速度保持不变 | B. | 周期和角速度保持不变 | ||
| C. | 合外力始终指向圆心 | D. | 合外力保持不变 |
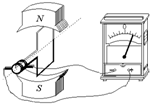
| A. | 指针随着线圈转动而摆动,并且线圈旋转一周,指针左右摆动一次 | |
| B. | 当线圈平面转到跟磁力线垂直的平面位置时,电流表的指针的偏转最大 | |
| C. | 当线圈平面转到跟磁力线平行的位置时,电流表的指针的偏转最大 | |
| D. | 在匀强磁场中匀速转动的线圈里产生感应电动势和感应电流是按正弦规律变化的 |
| A. | 50 N | B. | 500 N | C. | 500$\sqrt{2}$ N | D. | 10 00 N |
 光滑的$\frac{1}{4}$圆弧轨道固定在竖直平面内,与水平轨道CE连接.水平轨道的CD段光滑、DE段粗糙.一根轻质弹簧一端固定在C处的竖直面上,弹簧处于自然长度.将质量为m的物块a从顶端F点静止释放后,沿圆弧轨道下滑.
光滑的$\frac{1}{4}$圆弧轨道固定在竖直平面内,与水平轨道CE连接.水平轨道的CD段光滑、DE段粗糙.一根轻质弹簧一端固定在C处的竖直面上,弹簧处于自然长度.将质量为m的物块a从顶端F点静止释放后,沿圆弧轨道下滑. 如图所示,倾角为α的光滑固定斜面,斜面上相隔为d的平行虚线MN与PQ间有大小为B的匀强磁场,方向垂直斜面向下.一质量为m,电阻为R,边长为L的度v匀速进入磁场,线圈ab边刚进入磁场和cd边刚要离开磁场时,ab边两端的电压相等.已知磁场的宽度d大于线圈的边长L,重力加速度为g.求
如图所示,倾角为α的光滑固定斜面,斜面上相隔为d的平行虚线MN与PQ间有大小为B的匀强磁场,方向垂直斜面向下.一质量为m,电阻为R,边长为L的度v匀速进入磁场,线圈ab边刚进入磁场和cd边刚要离开磁场时,ab边两端的电压相等.已知磁场的宽度d大于线圈的边长L,重力加速度为g.求


