题目内容
如图所示,一质量为m =" 0.5" kg的小滑块,在F =" 4" N水平拉力的作用下,从水平面上的A处由静止开始运动,滑行s =" 1.75" m后由B处滑上倾角为37°的光滑斜面,滑上斜面后拉力的大小保持不变,方向变为沿斜面向上,滑动一段时间后撤去拉力。已知小滑块沿斜面上滑到的最远点C距B点为L =" 2" m,小滑块最后恰好停在A处。不计B处能量损失,g取10 m/s2,已知sin37° = 0.6 cos37° = 0.8。试求:

(1)小滑块与水平面间的动摩擦因数μ。
(2)小滑块在斜面上运动时,拉力作用的距离x。
(3)小滑块在斜面上运动时,拉力作用的时间t。

(1)小滑块与水平面间的动摩擦因数μ。
(2)小滑块在斜面上运动时,拉力作用的距离x。
(3)小滑块在斜面上运动时,拉力作用的时间t。
(1) μ=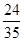 (2) x="1.25m(3)" t=0.5s。
(2) x="1.25m(3)" t=0.5s。
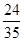 (2) x="1.25m(3)" t=0.5s。
(2) x="1.25m(3)" t=0.5s。根据滑块运动情况,依据动能定理,列方程解答。
解:(1)小滑块由C运动到A,由动能定理,mgsin37°·L-μmgs=0
解得小滑块与水平面间的动摩擦因数μ=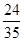 。
。
(2) 小滑块由A运动到C,由动能定理, Fs-μmgs+Fx- mgsin37°·L =0
解得小滑块在斜面上运动时,拉力作用的距离x=1.25m。
(3) 小滑块由A运动到C,由动能定理, Fs-μmgs=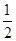 mv2,
mv2,
由牛顿第二定律,F- mgsin37° =ma
由运动学公式,x=vt+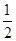 at2,
at2,
联立解得小滑块在斜面上运动时,拉力作用的时间t=0.5s
解:(1)小滑块由C运动到A,由动能定理,mgsin37°·L-μmgs=0
解得小滑块与水平面间的动摩擦因数μ=
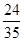 。
。(2) 小滑块由A运动到C,由动能定理, Fs-μmgs+Fx- mgsin37°·L =0
解得小滑块在斜面上运动时,拉力作用的距离x=1.25m。
(3) 小滑块由A运动到C,由动能定理, Fs-μmgs=
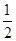 mv2,
mv2,由牛顿第二定律,F- mgsin37° =ma
由运动学公式,x=vt+
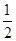 at2,
at2,联立解得小滑块在斜面上运动时,拉力作用的时间t=0.5s

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

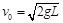 自N点滑向物块A,已知MN=L,AB间每次碰撞后即紧靠在一起但不粘连,每次AB与档板碰撞后均原速率弹回,求:
自N点滑向物块A,已知MN=L,AB间每次碰撞后即紧靠在一起但不粘连,每次AB与档板碰撞后均原速率弹回,求: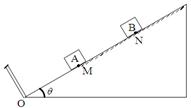
 ;
;

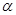 =53°,绳长l=2m的悬挂点O距水面的高度为H=3m。不考虑空气阻力和绳的质量,浮台露出水面的高度不计,水足够深。取g=10m/s2(sin53o=0.8,cos53o=0.6)。求:
=53°,绳长l=2m的悬挂点O距水面的高度为H=3m。不考虑空气阻力和绳的质量,浮台露出水面的高度不计,水足够深。取g=10m/s2(sin53o=0.8,cos53o=0.6)。求: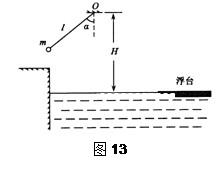
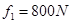 ,平均阻力
,平均阻力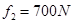 ,求选手落入水中的深度
,求选手落入水中的深度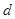 ;
;