题目内容
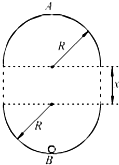
 如图所示,在同一竖直平面内两正对着的相同半圆光滑轨道,轨道半径R=2m,相隔一定的距离x,虚线沿竖直方向,一质量M=0.1kg的小球能在其间运动.今在最低点B与最高点A各放一个压力传感器,测试小球对轨道的压力,并通过计算机显示出来.已知小球在最低点B的速度为vB=20m/s,取g=10m/s2,不计空气阻力.求:
如图所示,在同一竖直平面内两正对着的相同半圆光滑轨道,轨道半径R=2m,相隔一定的距离x,虚线沿竖直方向,一质量M=0.1kg的小球能在其间运动.今在最低点B与最高点A各放一个压力传感器,测试小球对轨道的压力,并通过计算机显示出来.已知小球在最低点B的速度为vB=20m/s,取g=10m/s2,不计空气阻力.求:
(1)小球在最低点B对轨道的压力.
(2)小球能沿光滑轨道运动到最高点A时,x的最大值.
(3)若半圆轨道的间距x可在零到最大值之间变化,试在图中画出小球对轨道B、A两点的压力差随距离x变化的图象.
解:
(1)小球在最低点时,根据牛顿第二定律得
FB-Mg=M
代入解得FB=21N
又根据牛顿第三定律:小球在最低点B对轨道的压力为21N.
(2)小球恰好到达最高点A时,
Mg=M ①
①
小球从A到B的过程,根据机械能守恒定律得
Mg(2R+x)+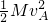 =
= ②
②
联立①②,代入解得 x=15m
(3)设小球对轨道B、A两点的压力大小分别为FB、FA.
以小球为研究对象,根据牛顿第二定律得
A点:Mg+FA=M ③
③
B点:FB-Mg=M ④
④
又Mg(2R+x)+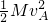 =
= ⑤
⑤
△FN=FB-FA ⑥
联立③④⑤⑥得
△FN=x+6
作图象如图.
答;
(1)小球在最低点B对轨道的压力为21N.
(2)小球能沿光滑轨道运动到最高点A时,x的最大值为15m.
(3)小球对轨道B、A两点的压力差随距离x变化的图象如图所示.
分析:(1)小球在最低点时,受到重力和轨道的支持力作用,两者的合力提供向心力,由牛顿第二定律求出支持力,再根据牛顿第三定律得到小球在最低点B对轨道的压力.
(2)当小球恰好到达最高点A时,x达到最大.此时由重力提供小球的向心力,由向心力公式列出A点速度表达式;小球从A到B的过程,只有重力做功,机械能守恒,由机械能守恒定律得出x的最大值.
(3)根据牛顿定律分别研究B、A两点的压力,得到压力之差的表达式,再画出图象.
点评:本题考查综合运用机械能守恒定律和牛顿定律分析动力学问题的能力.图象往往根据物理规律推导出解析式,再根据数学知识作图.
(1)小球在最低点时,根据牛顿第二定律得
FB-Mg=M

代入解得FB=21N
又根据牛顿第三定律:小球在最低点B对轨道的压力为21N.
(2)小球恰好到达最高点A时,
Mg=M
 ①
①小球从A到B的过程,根据机械能守恒定律得
Mg(2R+x)+
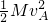 =
= ②
②联立①②,代入解得 x=15m
(3)设小球对轨道B、A两点的压力大小分别为FB、FA.
以小球为研究对象,根据牛顿第二定律得

A点:Mg+FA=M
 ③
③B点:FB-Mg=M
 ④
④又Mg(2R+x)+
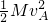 =
= ⑤
⑤△FN=FB-FA ⑥
联立③④⑤⑥得
△FN=x+6
作图象如图.
答;
(1)小球在最低点B对轨道的压力为21N.
(2)小球能沿光滑轨道运动到最高点A时,x的最大值为15m.
(3)小球对轨道B、A两点的压力差随距离x变化的图象如图所示.
分析:(1)小球在最低点时,受到重力和轨道的支持力作用,两者的合力提供向心力,由牛顿第二定律求出支持力,再根据牛顿第三定律得到小球在最低点B对轨道的压力.
(2)当小球恰好到达最高点A时,x达到最大.此时由重力提供小球的向心力,由向心力公式列出A点速度表达式;小球从A到B的过程,只有重力做功,机械能守恒,由机械能守恒定律得出x的最大值.
(3)根据牛顿定律分别研究B、A两点的压力,得到压力之差的表达式,再画出图象.
点评:本题考查综合运用机械能守恒定律和牛顿定律分析动力学问题的能力.图象往往根据物理规律推导出解析式,再根据数学知识作图.

练习册系列答案
相关题目
 如图所示,在同一竖直平面内有两个正对着的半圆形光滑轨道,轨道的半径都是R.轨道端点所在的水平线相隔一定的距离x.一质量为m的小球能在其间运动而不脱离轨道,经过最低点B时的速度为v.小球在最低点B与最高点A对轨道的压力之差为△F(△F>0),不计空气阻力.则( )
如图所示,在同一竖直平面内有两个正对着的半圆形光滑轨道,轨道的半径都是R.轨道端点所在的水平线相隔一定的距离x.一质量为m的小球能在其间运动而不脱离轨道,经过最低点B时的速度为v.小球在最低点B与最高点A对轨道的压力之差为△F(△F>0),不计空气阻力.则( )| A、m、x一定时,R越大,△F一定越大 | B、m、R一定时,x越大,△F一定越大 | C、m、x一定时,v越大,△F一定越大 | D、m、R一定时,v越大,△F一定越大 |
 质量4㎏的物体放在水平地面上,在一大小30N的水平外力作用下,恰能沿水平方向做匀速运动.求:
质量4㎏的物体放在水平地面上,在一大小30N的水平外力作用下,恰能沿水平方向做匀速运动.求: (2007?广东)如图所示,在同一竖直面上,质量为2m的小球A静止在光滑斜面的底部,斜面高度为H=2L.小球受到弹簧的弹性力作用后,沿斜面向上运动.离开斜面后,达到最高点时与静止悬挂在此处的小球B发生弹性碰撞,碰撞后球B刚好能摆到与悬点O同一高度,球A沿水平方向抛射落在水平面C上的P点,O点的投影O′与P的距离为L/2.已知球B质量为m,悬绳长L,视两球为质点,重力加速度为g,不计空气阻力,求:
(2007?广东)如图所示,在同一竖直面上,质量为2m的小球A静止在光滑斜面的底部,斜面高度为H=2L.小球受到弹簧的弹性力作用后,沿斜面向上运动.离开斜面后,达到最高点时与静止悬挂在此处的小球B发生弹性碰撞,碰撞后球B刚好能摆到与悬点O同一高度,球A沿水平方向抛射落在水平面C上的P点,O点的投影O′与P的距离为L/2.已知球B质量为m,悬绳长L,视两球为质点,重力加速度为g,不计空气阻力,求: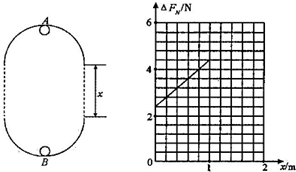 如图所示,在同一竖直平面内两正对着的半径为R的相同半圆光滑轨道,相隔一定的距离x,虚线沿竖直方向,一质量为m的小球能在其间运动.今在最低点B与最高点A各放一个压力传感器,测试小球对轨道的压力,并通过计算机显示出来.(不计空气阻力,g取10m/s2)
如图所示,在同一竖直平面内两正对着的半径为R的相同半圆光滑轨道,相隔一定的距离x,虚线沿竖直方向,一质量为m的小球能在其间运动.今在最低点B与最高点A各放一个压力传感器,测试小球对轨道的压力,并通过计算机显示出来.(不计空气阻力,g取10m/s2)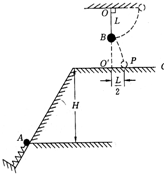 如图所示,在同一竖直平面上,质量为2m的小球A静止在光滑斜面的底部,斜面高度为H=2L,小球受到弹簧的弹性力作用后,沿斜面向上运动.离开斜面后,达到最高点时与静止悬挂在此处的小球B发生碰撞,碰撞中无机械能损失,碰撞后球B刚好能摆到与悬点O同一高度,球A沿水平方向抛射落在水平面C上的P点,O点的投影O'与P点的距离为L/2.已知球B质量为m,悬绳长L,视两球为质点,重力加速度为g,不计空气阻力,求:
如图所示,在同一竖直平面上,质量为2m的小球A静止在光滑斜面的底部,斜面高度为H=2L,小球受到弹簧的弹性力作用后,沿斜面向上运动.离开斜面后,达到最高点时与静止悬挂在此处的小球B发生碰撞,碰撞中无机械能损失,碰撞后球B刚好能摆到与悬点O同一高度,球A沿水平方向抛射落在水平面C上的P点,O点的投影O'与P点的距离为L/2.已知球B质量为m,悬绳长L,视两球为质点,重力加速度为g,不计空气阻力,求: