题目内容
 (2007?广东)如图所示,在同一竖直面上,质量为2m的小球A静止在光滑斜面的底部,斜面高度为H=2L.小球受到弹簧的弹性力作用后,沿斜面向上运动.离开斜面后,达到最高点时与静止悬挂在此处的小球B发生弹性碰撞,碰撞后球B刚好能摆到与悬点O同一高度,球A沿水平方向抛射落在水平面C上的P点,O点的投影O′与P的距离为L/2.已知球B质量为m,悬绳长L,视两球为质点,重力加速度为g,不计空气阻力,求:
(2007?广东)如图所示,在同一竖直面上,质量为2m的小球A静止在光滑斜面的底部,斜面高度为H=2L.小球受到弹簧的弹性力作用后,沿斜面向上运动.离开斜面后,达到最高点时与静止悬挂在此处的小球B发生弹性碰撞,碰撞后球B刚好能摆到与悬点O同一高度,球A沿水平方向抛射落在水平面C上的P点,O点的投影O′与P的距离为L/2.已知球B质量为m,悬绳长L,视两球为质点,重力加速度为g,不计空气阻力,求:(1)球B在两球碰撞后一瞬间的速度大小;
(2)球A在两球碰撞前一瞬间的速度大小;
(3)弹簧的弹性力对球A所做的功.
分析:两球碰撞过程满足动量守恒定律,B球上升过程满足机械能守恒定律或动能定理,A球碰撞后做平抛运动,A球从弹起到与B球碰撞可用动能定理.
解答:解:(1)碰撞后,根据机械能守恒定律,对B球有:mgL=
m
解得:vB=
即球B在两球碰撞后一瞬间的速度大小为
.
(2)A、B球碰撞水平方向动量守恒有:2m
=2m
+
?2m
=
?2m
+
?m
解得:vA=
v0=
即球A在两球碰撞前一瞬间的速度大小为
.
(3)碰后A球做平抛运动,设平抛高度为y,有:
=vAt y=
g
解得:y=L
对A球应用动能定理得:W-2mg(y+2L)=
?2m
解得:W=
mgL
即弹簧的弹性力对球A所做的功为
mgL.
| 1 |
| 2 |
| v | 2 B |
解得:vB=
| 2gL |
即球B在两球碰撞后一瞬间的速度大小为
| 2gL |
(2)A、B球碰撞水平方向动量守恒有:2m
| v | 0 |
| v | A |
| mv | B |
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
解得:vA=
| 1 |
| 4 |
| 2gL |
| 3 |
| 4 |
| 2gL |
即球A在两球碰撞前一瞬间的速度大小为
| 3 |
| 4 |
| 2gL |
(3)碰后A球做平抛运动,设平抛高度为y,有:
| L |
| 2 |
| 1 |
| 2 |
| t | 2 |
解得:y=L
对A球应用动能定理得:W-2mg(y+2L)=
| 1 |
| 2 |
| v | 2 0 |
解得:W=
| 57 |
| 8 |
即弹簧的弹性力对球A所做的功为
| 57 |
| 8 |
点评:解物理题的关键是正确分析物理过程,再根据不同过程选用相应的规律求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2007?广东)如图所示的匀强电场E的区域内,由A、B、C、D、A′、B′、C′、D′作为顶点构成一正方体空间,电场方向与面ABCD垂直.下列说法正确的是( )
(2007?广东)如图所示的匀强电场E的区域内,由A、B、C、D、A′、B′、C′、D′作为顶点构成一正方体空间,电场方向与面ABCD垂直.下列说法正确的是( )
 (2007?广东)如图所示,在倾角为θ的固定光滑斜面上,质量为m的物体受外力F1和F2的作用,F1方向水平向右,F2方向竖直向上.若物体静止在斜面上,则下列关系正确的是( )
(2007?广东)如图所示,在倾角为θ的固定光滑斜面上,质量为m的物体受外力F1和F2的作用,F1方向水平向右,F2方向竖直向上.若物体静止在斜面上,则下列关系正确的是( )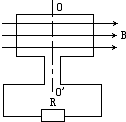 (2007?广东)如图所示,矩形线圈面积为S,匝数为N,内阻为r,绕OO′轴以角速度ω作匀速转动,在它从图示位置转过90°的过程中,下面说法正确的是( )
(2007?广东)如图所示,矩形线圈面积为S,匝数为N,内阻为r,绕OO′轴以角速度ω作匀速转动,在它从图示位置转过90°的过程中,下面说法正确的是( )