题目内容
8.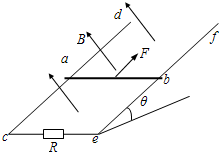 如图所示,有两根相距L的平行光滑金属导轨cd、ef与水平面成θ角固定放置,底端接一阻值为R的电阻.在轨道平面内有一匀强磁场,磁场方向垂直轨道平面斜向上.导轨上有一平行于ce并与导轨垂直的金属杆ab,质量为m.在沿导轨平面向上的恒定拉力F作用下,金属杆ab从底端ce由静止沿导轨向上运动,当速度达到最大值v后,撤去拉力F,求:(导轨足够长,导轨和金属杆的电阻均忽略不计,重力加速度为g)
如图所示,有两根相距L的平行光滑金属导轨cd、ef与水平面成θ角固定放置,底端接一阻值为R的电阻.在轨道平面内有一匀强磁场,磁场方向垂直轨道平面斜向上.导轨上有一平行于ce并与导轨垂直的金属杆ab,质量为m.在沿导轨平面向上的恒定拉力F作用下,金属杆ab从底端ce由静止沿导轨向上运动,当速度达到最大值v后,撤去拉力F,求:(导轨足够长,导轨和金属杆的电阻均忽略不计,重力加速度为g)(1)刚撤去外力F时金属杆所受安培力的大小与方向;
(2)磁场磁感应强度的大小;
(3)若最后ab杆又沿导轨匀速回到ce端,此时金属杆的速度为多大?
分析 (1)对杆受力分析,由共点力的平衡条件可求得安培力的大小和方向;
(2)根据导体切割磁感线规律可求得感应电流,由安培力公式可求得磁感应强度;
(3)最后匀速运动时,安培力与重力的分力相等,根据平衡关系可求得匀速的速度.
解答  解:(1)当ab杆沿导轨上滑达到最大速度v时,其受力如图所示
解:(1)当ab杆沿导轨上滑达到最大速度v时,其受力如图所示
由平衡条件可知:
F-F安-mgsinθ=0
所以安培力的大小为F安=F-mgsinθ
安培力的方向为垂直ab棒沿斜面向下
(2)安培力F安=BIL
感应电流 $I=\frac{E}{R}=\frac{BLv}{R}$
解得$B=\sqrt{\frac{(F-mgsinθ)R}{{{L^2}v}}}$
(3)要使匀速运动,则有$mgsinθ-{F_安}^′=0$
安培力为:${F_安}^′=BI'L$
感应电流为:
$I'=\frac{E'}{R}=\frac{BLv'}{R}$
由以上可解得$v'=\frac{mgvsinθ}{F-mgsinθ}$
答:(1)刚撤去外力F时金属杆所受安培力的大小为F-mgsinθ;方向垂直ab棒沿斜面向下;
(2)磁场磁感应强度的大小为$\sqrt{\frac{(F-mgsinθ)R}{{L}^{2}v}}$;
(3)若最后ab杆又沿导轨匀速回到ce端,此时金属杆的速度为$\frac{mgvsinθ}{F-mgsinθ}$
点评 该题为电磁感应与动力学综合的问题,解决本题的关键理清导体棒的运动情况,知道达到最大速度时,加速度为零,处于平衡状态.

练习册系列答案
相关题目
18. 科幻电影《星际穿越》中描述了空间站中模拟地球上重力的装置.这个模型可以简化为如图所示的环形实验装置,装置的外侧壁相当于“地板”.让环形实验装置绕O点旋转,能使“地板”上可视为质点的物体在地球表面处有同样的“重力”,已知地球表面重力加速度为g,装置的外半径为R,则旋转角速度应为( )
科幻电影《星际穿越》中描述了空间站中模拟地球上重力的装置.这个模型可以简化为如图所示的环形实验装置,装置的外侧壁相当于“地板”.让环形实验装置绕O点旋转,能使“地板”上可视为质点的物体在地球表面处有同样的“重力”,已知地球表面重力加速度为g,装置的外半径为R,则旋转角速度应为( )
 科幻电影《星际穿越》中描述了空间站中模拟地球上重力的装置.这个模型可以简化为如图所示的环形实验装置,装置的外侧壁相当于“地板”.让环形实验装置绕O点旋转,能使“地板”上可视为质点的物体在地球表面处有同样的“重力”,已知地球表面重力加速度为g,装置的外半径为R,则旋转角速度应为( )
科幻电影《星际穿越》中描述了空间站中模拟地球上重力的装置.这个模型可以简化为如图所示的环形实验装置,装置的外侧壁相当于“地板”.让环形实验装置绕O点旋转,能使“地板”上可视为质点的物体在地球表面处有同样的“重力”,已知地球表面重力加速度为g,装置的外半径为R,则旋转角速度应为( )| A. | $\sqrt{\frac{g}{R}}$ | B. | $\sqrt{\frac{R}{g}}$ | C. | 2$\sqrt{\frac{g}{R}}$ | D. | $\sqrt{\frac{2R}{g}}$ |
19. 质量为m的飞机以恒定速率v在空气水平盘旋,如图所示,其做匀速圆周运动的半径为R,重力加速度为g,则此时空气对飞机的作用力大小为( )
质量为m的飞机以恒定速率v在空气水平盘旋,如图所示,其做匀速圆周运动的半径为R,重力加速度为g,则此时空气对飞机的作用力大小为( )
 质量为m的飞机以恒定速率v在空气水平盘旋,如图所示,其做匀速圆周运动的半径为R,重力加速度为g,则此时空气对飞机的作用力大小为( )
质量为m的飞机以恒定速率v在空气水平盘旋,如图所示,其做匀速圆周运动的半径为R,重力加速度为g,则此时空气对飞机的作用力大小为( )| A. | m$\frac{{v}^{2}}{R}$ | B. | mg | C. | m$\sqrt{{g}^{2}+\frac{{v}^{4}}{{R}^{2}}}$ | D. | m$\sqrt{{g}^{2}-\frac{{v}^{4}}{{R}^{2}}}$ |
13.如图所示,某人由A点划船渡河,船头指向始终与河岸垂直,则下列说法正确的是( )


| A. | 小船能到达正对岸的B点 | |
| B. | 小船能到达正对岸B点的左侧 | |
| C. | 小船到达对岸的位置与水流速度有关 | |
| D. | 小船到达对岸的时间与水流速度无关 |
20. 如图所示,在载流直导线近旁固定有两平行光滑导轨A、B,导轨与直导线平行且在同一水平面内,在导轨上有两可自由滑动的导体ab和cd.当载流直导线中的电流逐渐增强时,导体ab和cd的运动情况是( )
如图所示,在载流直导线近旁固定有两平行光滑导轨A、B,导轨与直导线平行且在同一水平面内,在导轨上有两可自由滑动的导体ab和cd.当载流直导线中的电流逐渐增强时,导体ab和cd的运动情况是( )
 如图所示,在载流直导线近旁固定有两平行光滑导轨A、B,导轨与直导线平行且在同一水平面内,在导轨上有两可自由滑动的导体ab和cd.当载流直导线中的电流逐渐增强时,导体ab和cd的运动情况是( )
如图所示,在载流直导线近旁固定有两平行光滑导轨A、B,导轨与直导线平行且在同一水平面内,在导轨上有两可自由滑动的导体ab和cd.当载流直导线中的电流逐渐增强时,导体ab和cd的运动情况是( )| A. | 一起向左运动 | B. | 一起向右运动 | ||
| C. | 相背运动,相互远离 | D. | 相向运动,相互靠近 |
18. 如图所示,质量为m的木块从半径为R的固定半球形的碗口下滑到碗的最低点的过程中,如果由于摩擦力的作用使得木块做匀速圆周运动,则( )
如图所示,质量为m的木块从半径为R的固定半球形的碗口下滑到碗的最低点的过程中,如果由于摩擦力的作用使得木块做匀速圆周运动,则( )
 如图所示,质量为m的木块从半径为R的固定半球形的碗口下滑到碗的最低点的过程中,如果由于摩擦力的作用使得木块做匀速圆周运动,则( )
如图所示,质量为m的木块从半径为R的固定半球形的碗口下滑到碗的最低点的过程中,如果由于摩擦力的作用使得木块做匀速圆周运动,则( )| A. | 木块的加速度为零 | |
| B. | 木块的加速度不变 | |
| C. | 木块的速度不变 | |
| D. | 木块下滑过程中的加速度大小不变,方向时刻指向球心 |





 用图甲所示的装置研究光电效应现象,当用能量为5.0eV的光子照射光电管的阴极K时,测得电流计上的示数随电压变化的图象如图乙所示.则光电子的最大初动能为2eV,阴极K的截止频率为4.8×10-19Hz(电子的电荷量e=1.60×10-19C,普朗克常量h=6.63×10-34J.s.结果保留两位有效数字).
用图甲所示的装置研究光电效应现象,当用能量为5.0eV的光子照射光电管的阴极K时,测得电流计上的示数随电压变化的图象如图乙所示.则光电子的最大初动能为2eV,阴极K的截止频率为4.8×10-19Hz(电子的电荷量e=1.60×10-19C,普朗克常量h=6.63×10-34J.s.结果保留两位有效数字).