题目内容
一个物块放置在粗糙的水平地面上，受到的水平拉力F随时间t变化的关系如图（a）所示，速度v随时间t变化的关系如图（b）所示．取g=10m/s2，求：
（1）1s末物块所受摩擦力的大小f1；
（2）物块在前6s内的位移大小s；
（3）物块与水平地面间的动摩擦因数μ．
解：（1）从图（a）中可以读出，当t=1s时，f1=F1=4N
（2）物块在前6s内的位移大小s=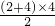
=12m
（3）从图（b）中可以看出，在t=2s至t=4s的过程中，物块做匀加速运动，加速度大小为
由牛顿第二定律，有
F2-μmg=ma
F3=f=μmg
所以 m=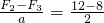
kg=2kg
由F3=f=μmg解得：
μ=
答：（1）1s末物块所受摩擦力的大小为4N；
（2）物块在前6s内的位移大小为12m；
（3）物块与水平地面间的动摩擦因数为0.4．
分析：（1）由图读出t1=1s时，物体处于静止状态，摩擦力的大小f等于水平拉力F；
（2）由速度-时间图象“面积”求出物块在前6s内的位移大小s；
（3）由图“斜率”求出加速度，根据牛顿第二定律求出质量．在4s～6s内，滑动摩擦力大小与拉力相等，由公式f=μN求出μ．
点评：本题首先考查读图能力，其次要根据速度图象分析物体的运动情况，这是解决本题的基础．
（2）物块在前6s内的位移大小s=
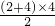=12m （3）从图（b）中可以看出，在t=2s至t=4s的过程中，物块做匀加速运动，加速度大小为
由牛顿第二定律，有
F2-μmg=ma
F3=f=μmg
所以 m=
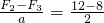kg=2kg由F3=f=μmg解得：
μ=
答：（1）1s末物块所受摩擦力的大小为4N；
（2）物块在前6s内的位移大小为12m；
（3）物块与水平地面间的动摩擦因数为0.4．
分析：（1）由图读出t1=1s时，物体处于静止状态，摩擦力的大小f等于水平拉力F；
（2）由速度-时间图象“面积”求出物块在前6s内的位移大小s；
（3）由图“斜率”求出加速度，根据牛顿第二定律求出质量．在4s～6s内，滑动摩擦力大小与拉力相等，由公式f=μN求出μ．
点评：本题首先考查读图能力，其次要根据速度图象分析物体的运动情况，这是解决本题的基础．
练习册系列答案
相关题目
一个物块放置在粗糙的水平地面上，受到的水平拉力F随时间t变化的关系如图（a）所示，速度v随时间t变化的关系如图（b）所示，求：
一个物块放置在粗糙的水平地面上，受到的水平拉力F随时间t变化的关系如图（a）所示．速度v随时间t变化的关系如图（b）所示（g=10m/s2）．求：
一个物块放置在粗糙的水平地面上，受到的水平拉力F随时间t变化的关系如图甲所示，速度v随时间t变化的关系如图乙所示，g=10m/s2，则由图中信息可判定（ ）
；