题目内容
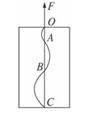
如图所示,螺旋形光滑轨道竖直放置,P、Q为对应的轨道最高点,一个小球以一定速度沿轨道切线方向进入轨道,且能过轨道最高点P,则下列说法中正确的是( )


| A.轨道对小球做正功,小球的线速度vp>vQ |
| B.轨道对小球不做功,小球的角速度ωP<ωQ |
| C.小球的向心加速度aP>aQ |
| D.轨道对小球的压力FP>FQ |
B
试题分析:由于支持力始终与速度方向垂直,所以支持力不做功即轨道对小球不做功,仅有重力做功,小球机械能守恒.则P点的线速度小于Q点线速度.故A错误;由于支持力始终与速度方向垂直,所以支持力不做功即轨道对小球不做功,仅有重力做功,小球机械能守恒.则P点的速度小于Q点速度,且P点的半径大于Q点的半径.所以小球通过P点的角速度小于通过Q点的.故B正确;由于支持力始终与速度方向垂直,所以支持力不做功即轨道对小球不做功,仅有重力做功,小球机械能守恒.则P点的速度小于Q点速度,且P点的半径大于Q点的半径.所以小球在P点的向心加速度小于Q点的,故C错误;由于支持力始终与速度方向垂直,所以支持力不做功即轨道对小球不做功,仅有重力做功,小球机械能守恒.则P点的速度小于Q点速度,且P点的半径大于Q点的 半径.所以小球在P点的向心加速度小于Q点的,则小球在P点的向心力小于Q点的,而向心力是由重力与轨道对它的支持力提供,因此小球在P点的支持力小于Q 点的,即小球对轨道的压力P点小于Q点的.故D错误;
故选:A
点评:小球在竖直放置的螺旋形轨道运动,速度时大时小,原因是动能与重力势能在相互转化.当在水平放置的光滑的螺旋形轨道运动时,由于支持力始终不做功,因此速度大小不变,随着轨迹半径越来越小,导致小球的角速度越来越大,转动的越来越快.

练习册系列答案
相关题目