Question

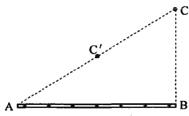
【题目】如图所示,AB为均匀带有电荷量为+Q的细棒,C为AB棒附近的一点,CB垂直于AB.AB棒上电荷形成的电场中C点的电势为φ0,φ0可以等效成AB棒上电荷集中于AB上某点P处、带电量为+Q的点电荷所形成的电场在C点的电势。若PC的距离为r,由点电荷电势的知识可知φ0=kQ/r. 若某点处在多个点电荷形成的电场中,则电势为每一个点电荷在该点所产生的电势的代数和。根据题中提供的知识与方法,我们可将AB棒均分成两段,并看成两个点电荷,就可以求得AC连线中点C′处的电势为

A. 2φ0 B. φ0 C. φ0 D. 4φ0

Answer 1

【答案】A

【解析】

设φ0等效成AB棒上的电荷集中于AB中点处，即AB的中点D到C的距离DC等于AD的中点E到C′的距离的一半；带电量为+Q的点电荷所形成的电场在C点的电势，将AB棒均分成两段，并看成两个点电荷，每个点电荷的电荷量为Q/2，由φ0=kQ/r可知，每个电荷量为Q/2的点电荷在C′点产生电势为φ0，两个点电荷在AC连线中点C′处的电势为2φ0，故A正确，BCD错误；故选A。