题目内容
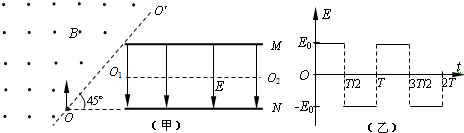
(2013?南通二模)如图甲所示,在边界OO′左侧区域有磁感应强度为B的匀强磁场,磁场方向水平向外.右侧水平放置长为L、相距为d的平行金属板M、N,M板左端紧靠磁场边界,磁场边界O点与N板在同一水平面上,边界OO′与水平面的夹角为45°,O1O2为平行板的中线,在两板间存在如图乙所示的交变电场(取竖直向下为正方向).某时刻从O点竖直向上同时发射两个质量均为m、电量均为+q粒子a和b,由于初速度不同,粒子a在图乙中的t=
时刻,从O1点进入板间电场运动,并从O2点射出板间电场;粒子b恰好紧靠M板进入电场,已知交变电场周期T=
,不计粒子重力和粒子间的相互作用.
(1)求粒子a、b从O点射出时的初速度va和vb.
(2)粒子b能穿出板间电场,求电场强度大小E0满足的条件.
(3)若粒子b刚好能穿出板间电场,求粒子b穿过板间电场过程中电场力做的功W.
| T |
| 4 |
| 4m |
| qB |
(1)求粒子a、b从O点射出时的初速度va和vb.
(2)粒子b能穿出板间电场,求电场强度大小E0满足的条件.
(3)若粒子b刚好能穿出板间电场,求粒子b穿过板间电场过程中电场力做的功W.

分析:(1)根据题意正确画出粒子在磁场中的运动的轨迹,在根据轨迹上的几何关系确定粒子运动的半径,由洛伦兹力提供向心力求得速度;
(2)根据牛顿第二定律求出加速度,进而确定粒子在电场中运动的规律,最后求出电场强度满足的条件;
(2)根据牛顿第二定律求出加速度,进而确定粒子在电场中运动的规律,最后求出电场强度满足的条件;
解答:解:(1)如图甲所示,粒子a、b在磁场中均转过90°,平行于金属板进入电场,设在磁场中回旋半径分别是ra和rb,则由几何关系有
ra=
; rb=d
由洛伦兹力提供向心力有:qvaB=
;qvbB=
解得va=
;vb=
(2)粒子a、b同时离开磁场,a比b进入电场落后的时间 △t=
解得 △t=
=
粒子b在t=0时刻进入电场,粒子在电场中运动的加速度:a=
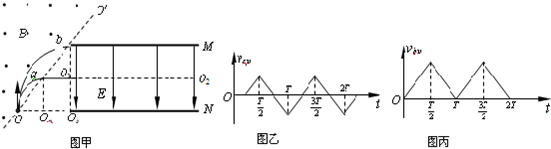
粒子a在竖直方向速度随时间的变化图象如图乙,在板间运动的时间:ta=
=kT(k为正整数)
粒子b在竖直方向速度随时间的变化图象如图丙,在板间运动的时间:tb=
=
粒子b在
内沿竖直方向运动的位移:y0=
a(
)2
粒子b能够穿出板间电场应满足 ky0≤d
解得E0≤
(3)由上述可知 E0=
粒子b在板间运动的时间 t0=
=k
则 k=
讨论:k是下列两种可能之一
①若k为偶数,粒子b在竖直方向的速度vy=0
则 W=0
②若k为奇数 W=qE0?
a(
)2
解得 W=
答:(1)粒子a、b从O点射出时的初速度va=
和vb=
.
(2)电场强度大小E0满足的条件E0≤
.
(3)粒子b穿过板间电场过程中电场力做的功W=
.
ra=
| d |
| 2 |
由洛伦兹力提供向心力有:qvaB=
m
| ||
| ra |
m
| ||
| rb |
解得va=
| qBd |
| 2m |
| qBd |
| m |
(2)粒子a、b同时离开磁场,a比b进入电场落后的时间 △t=
| d |
| 2va |
解得 △t=
| m |
| qB |
| T |
| 4 |
粒子b在t=0时刻进入电场,粒子在电场中运动的加速度:a=
| qE0 |
| m |
粒子a在竖直方向速度随时间的变化图象如图乙,在板间运动的时间:ta=
| L |
| va |
粒子b在竖直方向速度随时间的变化图象如图丙,在板间运动的时间:tb=
| L |
| vb |
| kT |
| 2 |
粒子b在
| T |
| 2 |
| 1 |
| 2 |
| T |
| 2 |
粒子b能够穿出板间电场应满足 ky0≤d
解得E0≤
| qd2B2 |
| mL |
(3)由上述可知 E0=
| qd2B2 |
| mL |
粒子b在板间运动的时间 t0=
| L |
| v0 |
| T |
| 2 |
则 k=
| L |
| 2d |
讨论:k是下列两种可能之一
①若k为偶数,粒子b在竖直方向的速度vy=0
则 W=0
②若k为奇数 W=qE0?
| 1 |
| 2 |
| T |
| 2 |
解得 W=
| 2q2d4B2 |
| mL2 |

答:(1)粒子a、b从O点射出时的初速度va=
| qBd |
| 2m |
| qBd |
| m |
(2)电场强度大小E0满足的条件E0≤
| qd2B2 |
| mL |
(3)粒子b穿过板间电场过程中电场力做的功W=
| 2q2d4B2 |
| mL2 |
点评:做好此类题目的关键是准确的画出粒子运动的轨迹图,利用几何知识求出粒子运动的半径,再结合半径公式和周期公式去分析,难度较大

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013?南通二模)一位参加达喀尔汽车拉力赛的选手驾车翻越了如图所示的沙丘,A、B、C、D为车在翻越沙丘过程中经过的四个点,车从坡的最高点B开始做平抛运动,无碰撞地落在右侧直斜坡上的C点,然后运动到平地上的D点.当地重力加速度为g,下列说法中正确的是( )
(2013?南通二模)一位参加达喀尔汽车拉力赛的选手驾车翻越了如图所示的沙丘,A、B、C、D为车在翻越沙丘过程中经过的四个点,车从坡的最高点B开始做平抛运动,无碰撞地落在右侧直斜坡上的C点,然后运动到平地上的D点.当地重力加速度为g,下列说法中正确的是( ) (2013?南通二模)某区域的电场线分布如图所示,其中间一根电场线是直线,一带正电的粒子从直线上的O点由静止开始在电场力作用下运动到A点.取O点为坐标原点,沿直线向右为x轴正方向,粒子的重力忽略不计.则在运动过程中,下列关于粒子运动速度v和加速度a随时间t的变化、粒子的动能Ek和运动径迹上电势φ随位移x的变化图线可能正确的是( )
(2013?南通二模)某区域的电场线分布如图所示,其中间一根电场线是直线,一带正电的粒子从直线上的O点由静止开始在电场力作用下运动到A点.取O点为坐标原点,沿直线向右为x轴正方向,粒子的重力忽略不计.则在运动过程中,下列关于粒子运动速度v和加速度a随时间t的变化、粒子的动能Ek和运动径迹上电势φ随位移x的变化图线可能正确的是( ) (2013?南通二模)某同学用频闪相机拍摄了运动员跳远比赛时助跑、起跳、最高点、落地四个位置的照片,简化图如图所示.则运动员起跳瞬间消耗的体能最接近( )
(2013?南通二模)某同学用频闪相机拍摄了运动员跳远比赛时助跑、起跳、最高点、落地四个位置的照片,简化图如图所示.则运动员起跳瞬间消耗的体能最接近( ) (2013?南通二模)某同学设计的散热排风控制电路如图所示,M为排风扇,R是可变电阻,R0是半导体热敏电阻,其阻值随温度升高而减小.控制开关电路具有下列特性:当A点电势φA<φ0时,控制开关处于断路状态;当φA≥φ0时,控制开关接通电路,M开始运转.下列说法中正确的是( )
(2013?南通二模)某同学设计的散热排风控制电路如图所示,M为排风扇,R是可变电阻,R0是半导体热敏电阻,其阻值随温度升高而减小.控制开关电路具有下列特性:当A点电势φA<φ0时,控制开关处于断路状态;当φA≥φ0时,控制开关接通电路,M开始运转.下列说法中正确的是( )