题目内容
5.两块平行金属板之间有一匀强电场,不同的带电粒子都以垂直于电场线的方向飞入这一匀强电场.为使其通过这一电场时他们的横向偏移量相同,它们进入电场之前应该具有( )| A. | 相同的动能,相同的荷质比 | |
| B. | 相同的动量,相同的荷质比 | |
| C. | 相同的速度,相同的荷质比 | |
| D. | 先由静止开始,经同一电场加速后进入该偏转电场 |
分析 粒子在电场中做类平抛运动,根据类平抛运动知识求解出侧移量的表达式,根据表达式讨论结果跟哪些因素有关.
解答 解:ABC、令粒子的质量为m、所带电荷量为q,金属板长为L,板间电场为E,粒子入射速度为v0,则根据分运动公式,有:
L=v0t
y=$\frac{1}{2}a{t}^{2}$
其中:a=$\frac{qE}{m}$
解得:y=$\frac{qE{L}^{2}}{2m{v}_{0}^{2}}$ ①
要使不同的带电粒子的侧移量相等,需要比荷相等且速度相等,故AB错误,C正确;
D、先由静止开始,经同一电场加速后进入该偏转电场,加速过程,有:
qU1=$\frac{1}{2}m{v}_{0}^{2}$ ②
联立①②解得:
y=$\frac{E{L}^{2}}{4{U}_{1}}$
侧移量y与粒子的比荷无关,故轨迹相同;故D正确;
故选:CD
点评 能用运动的合成与分解的方法求出粒子侧移量的表达式,根据题设给出的条件由表达式进行分析,比荷为带电微粒所带电荷与质量的比值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10. 如图所示,质量为m的小球用水平轻弹簧系住,并用倾角为45°的光滑木板托住,小球恰好处于静止状态,木板只与小球接触,当木板突然向下撤离的瞬间,小球的加速度为( )
如图所示,质量为m的小球用水平轻弹簧系住,并用倾角为45°的光滑木板托住,小球恰好处于静止状态,木板只与小球接触,当木板突然向下撤离的瞬间,小球的加速度为( )
 如图所示,质量为m的小球用水平轻弹簧系住,并用倾角为45°的光滑木板托住,小球恰好处于静止状态,木板只与小球接触,当木板突然向下撤离的瞬间,小球的加速度为( )
如图所示,质量为m的小球用水平轻弹簧系住,并用倾角为45°的光滑木板托住,小球恰好处于静止状态,木板只与小球接触,当木板突然向下撤离的瞬间,小球的加速度为( )| A. | $\sqrt{2}g$ | B. | $\sqrt{3}g$ | C. | g | D. | 0 |
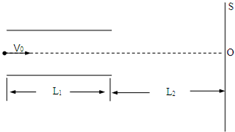 如图所示,C为平行板电容器,虚线到两极板距离相等,极板长L1=8.0×10-2m,两板间距d=1.0×10-2m.S为屏,与极板垂直,到极板的距离L2=0.16m.有一细电子束沿图中虚线以速度V0=8.0×106m/s连续不断地射入C.已知电子电荷量e=1.6×10-19C,电子质量m=9.0×10-31kg.忽略电子所受的重力,不考虑电容器边缘电场的变化,电容器外部的电场为零.
如图所示,C为平行板电容器,虚线到两极板距离相等,极板长L1=8.0×10-2m,两板间距d=1.0×10-2m.S为屏,与极板垂直,到极板的距离L2=0.16m.有一细电子束沿图中虚线以速度V0=8.0×106m/s连续不断地射入C.已知电子电荷量e=1.6×10-19C,电子质量m=9.0×10-31kg.忽略电子所受的重力,不考虑电容器边缘电场的变化,电容器外部的电场为零. 在倾角30°的光滑斜面上并排放着质量分别是mA=5kg和mB=1kg的A、B两物块,劲度系数k=200N/m的轻弹簧一端与物块B相连,另一端与固定挡板相连,整个系统处于静止状态,现对A施加一沿斜面向上的力F,使物块A沿斜面向上作匀加速运动,已知力F在前0.2s内为变力,0.2s后为恒力,g取10m/s2,求F的最大值和最小值.
在倾角30°的光滑斜面上并排放着质量分别是mA=5kg和mB=1kg的A、B两物块,劲度系数k=200N/m的轻弹簧一端与物块B相连,另一端与固定挡板相连,整个系统处于静止状态,现对A施加一沿斜面向上的力F,使物块A沿斜面向上作匀加速运动,已知力F在前0.2s内为变力,0.2s后为恒力,g取10m/s2,求F的最大值和最小值.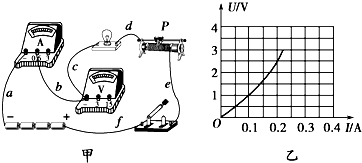 在做“描绘小灯泡的伏安特性曲线”的实验时,所用器材有:电动势为6V的电源,额定电压为2.5V的小灯泡,以及符合实验要求的滑动变阻器、电流表、电压表、开关和导线,要求能测出尽可能多的数据,图甲所示是没有连接完的实物电路.(已连接好的导线有a、b、c、d、e、f六根)
在做“描绘小灯泡的伏安特性曲线”的实验时,所用器材有:电动势为6V的电源,额定电压为2.5V的小灯泡,以及符合实验要求的滑动变阻器、电流表、电压表、开关和导线,要求能测出尽可能多的数据,图甲所示是没有连接完的实物电路.(已连接好的导线有a、b、c、d、e、f六根)