��Ŀ����
1��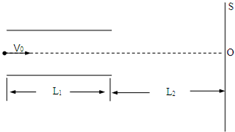 ��ͼ��ʾ��CΪƽ�а�����������ߵ������������ȣ����峤L1=8.0��10-2m��������d=1.0��10-2m��SΪ�����뼫�崹ֱ��������ľ���L2=0.16m����һϸ��������ͼ���������ٶ�V0=8.0��106m/s�������ϵ�����C����֪���ӵ����e=1.6��10-19C����������m=9.0��10-31kg�����Ե������ܵ������������ǵ�������Ե�糡�ı仯���������ⲿ�ĵ糡Ϊ�㣮
��ͼ��ʾ��CΪƽ�а�����������ߵ������������ȣ����峤L1=8.0��10-2m��������d=1.0��10-2m��SΪ�����뼫�崹ֱ��������ľ���L2=0.16m����һϸ��������ͼ���������ٶ�V0=8.0��106m/s�������ϵ�����C����֪���ӵ����e=1.6��10-19C����������m=9.0��10-31kg�����Ե������ܵ������������ǵ�������Ե�糡�ı仯���������ⲿ�ĵ糡Ϊ�㣮��1�����������ĵ��Ʋ�U1=5.4V���жϵ����Ƿ��ܹ�������������
��2�����������ĵ��Ʋ�U2=2.7V������ӵ�����S��ʱ������O��ľ��룮
���� ��1�����������ĵ��Ʋ�U1=5.4Vʱ�����ӽ���糡������ƽ���˶��������ܹ�����������˶��������ֽⷨ�����ݷ��˶���ʽ��ʽ�������������жϼ��ɣ�
��2�����������ĵ��Ʋ�U2=2.7V�����ӽ���糡������ƽ���˶����뿪�糡��������ֱ���˶�������ƽ���˶����̣����ݷ��˶���ʽ����ٶ�ƫת�ǵ�����ֵ�������켣����ϼ��ι�ϵ���з�����⣮
��� �⣺��1���������ĵ��Ʋ�U1=5.4Vʱ����������ܹ��������������ƽ���˶��ķ��˶���ʽ���У�
L1=v0t
$y=\frac{1}{2}a{t}^{2}$
����
a=$\frac{e{U}_{1}}{md}$
������ã�
$y=\frac{{e{U_1}L_1^2}}{2mdv_0^2}=\frac{{1.6��1{0^{-19}}��5.4��{{��8��1{0^{-2}}��}^2}}}{{2��9��1{0^{-31}}��1��1{0^{-2}}��{{��8��1{0^6}��}^2}}}=4.8��1{0^{-3}}m$
����y$��\frac{d}{2}$�����ܹ�������壻
��2���������ĵ��Ʋ�U2=2.7V������ƽ���˶����̣��У�
vx=v0
vy=at
����
a=$\frac{e{U}_{2}}{md}$
���ٶ�ƫת�ǵ�����ֵΪ��
tan��=$\frac{{v}_{y}}{{v}_{x}}$=$\frac{e{U}_{2}L}{md{v}_{0}^{2}}$
�����˶��켣����ͼ��ʾ��
��ϼ��ι�ϵ���У�
y=��$\frac{{L}_{1}}{2}+{L}_{2}$��tan��
������ã�
y=��$\frac{{L}_{1}}{2}+{L}_{2}$��$\frac{e{U}_{2}L}{md{v}_{0}^{2}}$=$��\frac{1}{2}��8��1{0^{-2}}+0.16����\frac{{1.6��1{0^{-19}}��2.7����8��1{0^{-2}}��}}{{9��1{0^{-31}}��1��1{0^{-2}}��{{��8��1{0^6}��}^2}}}=1.2��1{0^{-2}}m$
�𣺣�1�����������ĵ��Ʋ�U1=5.4V�������ܹ�������������
��2�����������ĵ��Ʋ�U2=2.7V�����ӵ�����S��ʱ������O��ľ���Ϊ1.2��10-2m��
���� �������ؿ�����������ڵ糡�е�ƫת���⣬Ҫ���������˶��ķֽⷨ�о���ƽ���˶�������ţ�ٵڶ����ɡ��˶�ѧ��ʽ����ѧ֪ʶ�õ��ۺ�ʽ���ٽ�����⣬����֮�пɲ������ݣ��Ӷ���С��������

 ������ϰ�ο����뵥Ԫ���ϵ�д�
������ϰ�ο����뵥Ԫ���ϵ�д� �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д�| A�� | ��ͬ�Ķ��ܣ���ͬ�ĺ��ʱ� | |
| B�� | ��ͬ�Ķ�������ͬ�ĺ��ʱ� | |
| C�� | ��ͬ���ٶȣ���ͬ�ĺ��ʱ� | |
| D�� | ���ɾ�ֹ��ʼ����ͬһ�糡���ٺ�����ƫת�糡 |

 5��0m/s��A������б������£�С��鵽��C��ʱ�ٶ�
5��0m/s��A������б������£�С��鵽��C��ʱ�ٶ� ��ȡ
��ȡ ��
��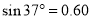 ��
��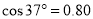
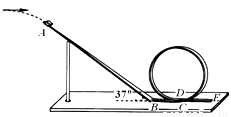
 ������һ����ֱ����
������һ����ֱ����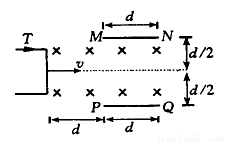
 ���ڴֲ�ˮƽ·���ϵĿ��ABCD������ΪM=30kg����б��AC����Ǧ�=37�㣬�������һ����⻬������Ϊm=20kg�����壬��ܾ�ֹʱ�������붥��AB����һ��С�ļ�϶����϶ԶС������İ뾶�ɺ��Բ��ƣ������������ˮƽ���������F=400N��������������v=16m/s���ٶ�������ֱ���˶���sin37��=0.6��cos37��=0.8��gȡ10m/s2����
���ڴֲ�ˮƽ·���ϵĿ��ABCD������ΪM=30kg����б��AC����Ǧ�=37�㣬�������һ����⻬������Ϊm=20kg�����壬��ܾ�ֹʱ�������붥��AB����һ��С�ļ�϶����϶ԶС������İ뾶�ɺ��Բ��ƣ������������ˮƽ���������F=400N��������������v=16m/s���ٶ�������ֱ���˶���sin37��=0.6��cos37��=0.8��gȡ10m/s2����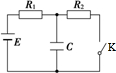 ��ͼ��ʾ��·E=10V��R1=4����R2=6����C=30��F����Դ����ɺ��ԣ���
��ͼ��ʾ��·E=10V��R1=4����R2=6����C=30��F����Դ����ɺ��ԣ���