题目内容
19.如图甲所示,一质量M=2kg,长为L的圆管竖直放置,顶端塞有质量为m=1kg的弹性小球.t=0时让管从静止自由下落,t=1.0s时落地,落地后管立刻以与落地时大小相等的速率竖直弹起,第一次弹起后管上升过程的速度图象如图乙所示(竖直向下为正方向).之后管每次落地后,总以与落地时相等的速率竖直弹起.已知小球始终没有从管中滑出,球与管间的滑动摩擦力等于最大静摩擦力,不计空气阻力及圆管与地面间碰撞的时间,求:(g=10m/s2)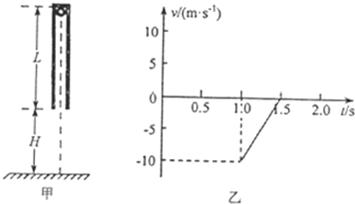
(1)球和管间的滑动摩擦力的大小;
(2)管从第一次落地到第二次落地所用的时间;
(3)圆管的最小长度.
分析 (1)乙图中t=1.0-1.5s内,管向上弹起做匀减速运动,由图象的斜率求出管的加速度,根据牛顿第二定律求球和管间的滑动摩擦力.
(2)根据牛顿第二定律和速度公式求第一次碰撞后管与球的速度相等的过程经历的时间,以及共同速度.由速度位移关系公式求出管上升的高度.由位移公式求出从速度第一次相等到第二次落地,管与球再次共同运动所经历的时间,从而得到总时间.
(3)圆管的最小长度时,球与管均静止,且球恰好在管的最下端,根据能量守恒定律求解.
解答 解:(1)由图乙可知,向下为正方向,在t2=1.5s-1.0s=0.5s内,管的加速度为
a1=$\frac{{v}_{0}}{{t}_{2}}$=$\frac{10}{0.5}$=20m/s2.
设球和管间的滑动摩擦力大小为f,由牛顿第二定律得:
Mg+f=Ma1,解得 f=20N
(2)在第一次碰撞后到管与球速度(设为v)相等的过程中,设球的加速度为a2,时间为t3,管上升的高度为h,由牛顿第二定律得:
mg-f=ma2,解得 a2=-10m/s2.
又对球有:v=v0+a2t3
对管有:v=-v0+a1t3
联立解得 t3=$\frac{2}{3}$s,v=$\frac{10}{3}$m/s
对管有:${v}^{2}-{v}_{0}^{2}$=-2a1h
从速度第一次相等到第二次落地,管与球再次共同运动,设该过程的时间为t4,则有
h=vt4+$\frac{1}{2}g{t}_{4}^{2}$
解得 t4=$\frac{\sqrt{5}-1}{3}$s
则管从第一次落地到第二次落地所用的时间 t=t3+t4=$\frac{\sqrt{5}+1}{3}$s
(3)设管的最小长度为L,最终管与球均静止时,球恰好在管的最下端,由能量守恒定律得:
MgH+mg(H+L)=fL
H=$\frac{1}{2}g{t}^{2}$
解得 L=15m
答:
(1)球和管间的滑动摩擦力的大小是20N;
(2)管从第一次落地到第二次落地所用的时间是$\frac{\sqrt{5}+1}{3}$s;
(3)圆管的最小长度是15m.
点评 本题的难点在于管和球的运动情况难于判断,关键通过计算理清球和管的运动规律,结合牛顿第二定律和运动学公式进行求解.

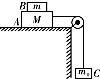 A,B、C三物块分别为M、m和m0,作如图所示的联结,绳子不可伸长,且绳子和滑轮的质量、滑轮的摩擦均可不计,若B随A一起沿水平桌面做匀速运动.则可以断定( )
A,B、C三物块分别为M、m和m0,作如图所示的联结,绳子不可伸长,且绳子和滑轮的质量、滑轮的摩擦均可不计,若B随A一起沿水平桌面做匀速运动.则可以断定( )| A. | 物块A与桌面之间有摩擦力,大小为m0g | |
| B. | 物块A与B之间有摩擦力,大小为m0g | |
| C. | 桌面对A、B对A都有摩擦力,两者方向相同,合力为m0g | |
| D. | 桌面对A有摩擦力,B对A摩擦力为0 |
| A. | 合力可以比每个分都大,也可以比两个分力都小 | |
| B. | 合力的作用效果与分力共同作用的效果相同 | |
| C. | 对一个已知力进行分解,有无数组分力的值 | |
| D. | 合力的大小不可能和它的分力大小相等 |
| A. | 重力就是地球的吸引力,方向竖直向下 | |
| B. | 形状规则的物体重心位置在几何中心 | |
| C. | 滑动摩擦力一定阻碍物体的相对运动 | |
| D. | 地球的物体不可能受到静摩擦力 |
 如图所示,水平传送带由电动机带动,始终以速度v匀速运动,质量为m的物体由静止释放,在水平传送带上,物体与传送带间的动摩擦因数为μ,物体最终与传送带保持相对静止,对于物体从静止释放到相对传送带静止这一过程,下列说法正确的是( )
如图所示,水平传送带由电动机带动,始终以速度v匀速运动,质量为m的物体由静止释放,在水平传送带上,物体与传送带间的动摩擦因数为μ,物体最终与传送带保持相对静止,对于物体从静止释放到相对传送带静止这一过程,下列说法正确的是( )| A. | 摩擦力对物块做的功为mv2 | B. | 摩擦力产生的热量为$\frac{1}{2}m{v}^{2}$ | ||
| C. | 传送带克服摩擦力做功为$\frac{1}{2}m{v}^{2}$ | D. | 电动机增加的功率为μmgv |
| A. | 2.0×104N/m | B. | 3.0×104N/m | C. | 1.0×104N/m | D. | 1.25×105N/m |
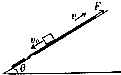 如图所示,在倾角θ=37°的足够长的斜面上,有质量m1=2kg的长木板.开始时,长木板上有一质量m2=1kg的小铁块(视为质点)以相对地面的初速度v0=1m/s从长木板的最上端沿长木板向下滑动,同时长木板在沿斜面向上的拉力F的作用下始终做速度v=0.6m/s的匀速运动,小铁块最终与长木板一起沿斜面向上做匀速运动.已知小铁块与长木板、长木板与斜面间的动摩擦因数均为μ=0.8,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.
如图所示,在倾角θ=37°的足够长的斜面上,有质量m1=2kg的长木板.开始时,长木板上有一质量m2=1kg的小铁块(视为质点)以相对地面的初速度v0=1m/s从长木板的最上端沿长木板向下滑动,同时长木板在沿斜面向上的拉力F的作用下始终做速度v=0.6m/s的匀速运动,小铁块最终与长木板一起沿斜面向上做匀速运动.已知小铁块与长木板、长木板与斜面间的动摩擦因数均为μ=0.8,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8. 如图所示,虚线1、2、3、4为静电场中的等势面,相邻的等势面之间的电势差相等,其中等势面3的电势为0,一电子仅在静电力的作用下运动,经过a点时的电势能为-8eV,则等势面2的电势φ2=4V,等势面4的电势φ4=-4V;若电子在经过等势面4上的b点时的动能为12eV,则当电子的动能为9eV,具有的电势能为7eV.
如图所示,虚线1、2、3、4为静电场中的等势面,相邻的等势面之间的电势差相等,其中等势面3的电势为0,一电子仅在静电力的作用下运动,经过a点时的电势能为-8eV,则等势面2的电势φ2=4V,等势面4的电势φ4=-4V;若电子在经过等势面4上的b点时的动能为12eV,则当电子的动能为9eV,具有的电势能为7eV.