题目内容
如图(甲)所示,质量分别为m=1kg、M=2kg的A、B两个小物块,用轻弹簧相连而静止在光滑水平面上,在A的左侧某处另有一质量也为m=1kg的小物块C,以v0=4m/s的速度正对A向右做匀速直线运动,一旦与A接触就将黏合在一起运动(黏合时间极短).若在C与A接触前,瞬间使A获得一初速度vA0,并从此时刻开始计时,规定向右为正方向,A的速度随时间变化的图象如图(乙)所示(此图象仅限C与A接触前),弹簧始终未超出弹性限度,vA0=6m/s.求:
(1)在C与A接触前,当A的速度分别为6m/s、2m/s、-2m/s时,求对应状态下B的速度,并据此在图(乙)中粗略画出B的速度随时间变化的图象(要求画出IT时间内).
(2)当A的速度为vA时C与A接触,在接触后的运动过程中弹簧的弹性势能为Ep,当vA取何值时,Ep有最大值?试求出Ep的最大值.

(1)在C与A接触前,当A的速度分别为6m/s、2m/s、-2m/s时,求对应状态下B的速度,并据此在图(乙)中粗略画出B的速度随时间变化的图象(要求画出IT时间内).
(2)当A的速度为vA时C与A接触,在接触后的运动过程中弹簧的弹性势能为Ep,当vA取何值时,Ep有最大值?试求出Ep的最大值.

分析:(1)研究A、B系统,由动量守恒定律求解B的速度
(2)当A、B、C具有相同的速度u时弹簧的弹性势能EP最大,由动量守恒和能量守恒定律求解.
(2)当A、B、C具有相同的速度u时弹簧的弹性势能EP最大,由动量守恒和能量守恒定律求解.
解答: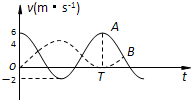 解:(1)由动量守恒定律可得:
解:(1)由动量守恒定律可得:
mvA0=mvA+MvB ①
由①式可得:vB=
(vA0-vA)②
代入vA=6m/s、2m/s、-2m/s时,得到对应的
VB=0、2m/s、4m/s
描给的图象如答图所示
(2)无论C与A如何接触,当A、B、C具有相同的速度u时弹簧的弹性势能EP最大.
由动量守恒定律可得:
mv0+mvA0=(2m+M)u ③
由③式解得:u=2.5(m/s)
设C与A碰撞前后A的瞬时速度分别为vA、v,碰撞过程中损失的机械能为△E,
由动量守恒和能量守恒定律可得:
mv0+mvA=2mv ④
△E=
mv02+
mvA2-
×2mv2⑤
由④⑤式可得:△E=
m(v0-vA)2⑥
设弹簧的最大弹性势能为EP,由能量守恒可得
mv02+
mvA_2=
×(2m+M)u2+△E+Ep⑦
由⑦式可得:Ep=
mv02+
mvA_2-
×(2m+M)u2-
×m(v0-vA)2⑧
由⑧式得:当vA=v0时C与A接触而黏在一起,此时不损失机械能,△E=0,
EP有最大值EPmax,将数据代入⑧式可得:
EPmax=13.5(J)
答:(1)对应状态下B的速度分别是0、2m/s、4m/s,
(2)当vA取4m/s时,Ep有最大值,Ep的最大值是13.5(J).
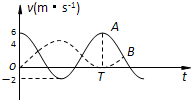 解:(1)由动量守恒定律可得:
解:(1)由动量守恒定律可得:mvA0=mvA+MvB ①
由①式可得:vB=
| m |
| M |
代入vA=6m/s、2m/s、-2m/s时,得到对应的
VB=0、2m/s、4m/s
描给的图象如答图所示
(2)无论C与A如何接触,当A、B、C具有相同的速度u时弹簧的弹性势能EP最大.
由动量守恒定律可得:
mv0+mvA0=(2m+M)u ③
由③式解得:u=2.5(m/s)
设C与A碰撞前后A的瞬时速度分别为vA、v,碰撞过程中损失的机械能为△E,
由动量守恒和能量守恒定律可得:
mv0+mvA=2mv ④
△E=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由④⑤式可得:△E=
| 1 |
| 4 |
设弹簧的最大弹性势能为EP,由能量守恒可得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由⑦式可得:Ep=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
由⑧式得:当vA=v0时C与A接触而黏在一起,此时不损失机械能,△E=0,
EP有最大值EPmax,将数据代入⑧式可得:
EPmax=13.5(J)
答:(1)对应状态下B的速度分别是0、2m/s、4m/s,
(2)当vA取4m/s时,Ep有最大值,Ep的最大值是13.5(J).
点评:对于这类弹簧问题注意用动态思想认真分析物体的运动过程,注意过程中的功能转化关系;解答时注意动量守恒和能量守恒列式分析求解.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
 如图(甲)所示,质量为m=50g,长l=10cm的铜棒,用长度也为l的两根轻软导线水平悬吊在竖直向上的匀强磁场中,磁感应强度B=1/3T.未通电时,轻线在竖直方向,通入恒定电流后,棒向外偏转的最大角度θ=37°,求此棒中恒定电流的大小.
如图(甲)所示,质量为m=50g,长l=10cm的铜棒,用长度也为l的两根轻软导线水平悬吊在竖直向上的匀强磁场中,磁感应强度B=1/3T.未通电时,轻线在竖直方向,通入恒定电流后,棒向外偏转的最大角度θ=37°,求此棒中恒定电流的大小. 如图(甲)所示,质量不计的弹簧竖直固定在水平面上,t=0时刻,将一金属小球从弹簧正上方某一高度处由静止释放,小球落到弹簧上压缩弹簧到最低点,然后又被弹起离开弹簧,上升到一定高度后再下落,如此反复,通过安装在弹簧下端的压力传感器,测出这一过程弹簧弹力F随时间,变化的图象如图(乙)所示,则( )
如图(甲)所示,质量不计的弹簧竖直固定在水平面上,t=0时刻,将一金属小球从弹簧正上方某一高度处由静止释放,小球落到弹簧上压缩弹簧到最低点,然后又被弹起离开弹簧,上升到一定高度后再下落,如此反复,通过安装在弹簧下端的压力传感器,测出这一过程弹簧弹力F随时间,变化的图象如图(乙)所示,则( )
 如图(甲)所示,质量m=0.5kg,初速度υ0=10m/s的物体,受到一个与初速方向相反的外力F的作用,沿粗糙的水平面滑动,经3s撤去外力,直到物体停止,整个过程物体的υ-t图象如图(乙)所示,g取10m/s2,则下列判断正确的是( )
如图(甲)所示,质量m=0.5kg,初速度υ0=10m/s的物体,受到一个与初速方向相反的外力F的作用,沿粗糙的水平面滑动,经3s撤去外力,直到物体停止,整个过程物体的υ-t图象如图(乙)所示,g取10m/s2,则下列判断正确的是( ) 如图(甲)所示,质量为M、长L=1.0m、右端带有竖直挡板的木板B,静止在光滑水平面上.质量为m的小木块(可视为质点)A,以水平速度v0=4.0m/s滑上B的左端,在右端与B碰撞后,最后恰好滑回木板B的左端.已知
如图(甲)所示,质量为M、长L=1.0m、右端带有竖直挡板的木板B,静止在光滑水平面上.质量为m的小木块(可视为质点)A,以水平速度v0=4.0m/s滑上B的左端,在右端与B碰撞后,最后恰好滑回木板B的左端.已知