题目内容
 如图(甲)所示,质量为M、长L=1.0m、右端带有竖直挡板的木板B,静止在光滑水平面上.质量为m的小木块(可视为质点)A,以水平速度v0=4.0m/s滑上B的左端,在右端与B碰撞后,最后恰好滑回木板B的左端.已知
如图(甲)所示,质量为M、长L=1.0m、右端带有竖直挡板的木板B,静止在光滑水平面上.质量为m的小木块(可视为质点)A,以水平速度v0=4.0m/s滑上B的左端,在右端与B碰撞后,最后恰好滑回木板B的左端.已知| M | m |
(1)木块A与木板B间的动摩擦因数;
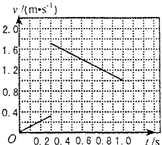
(2)在图(乙)所给坐标系中,画出此过程中B对地的速度--时间图线.
分析:(1)根据动量守恒定律求出A、B的共同速度,通过摩擦产生的热量等于系统动能的损失,根据能量守恒定律求出木块A与木板B间的动摩擦因数.
(2)A在B上向右滑行时,木板做匀加速运动,碰撞后反弹,木板做匀减速直线运动,根据动量守恒定律、牛顿第二定律和运动学公式求出碰撞前的末速度和时间以及匀减速运动的末速度和时间,从而作出速度时间图线.
(2)A在B上向右滑行时,木板做匀加速运动,碰撞后反弹,木板做匀减速直线运动,根据动量守恒定律、牛顿第二定律和运动学公式求出碰撞前的末速度和时间以及匀减速运动的末速度和时间,从而作出速度时间图线.
解答:解:(1)A、B共同运动时速度相等mv0=(m+M)v…①
木块A运动到B的右端时速度为v1,木板B的速度为V1,木板发生位移为s1,μmgs1=
M
-0
-μmg(s1+L)=
m
-
m
…②
木块A与B碰撞后速度为v2,木板B的速度为V2,A运动到B的左端时,B发生位移为s2-μmgs2=
M
-
M
μmg(s2-L)=
m
-
m
…③
由于碰撞前后机械能守恒
m
+
M
=
m
+
M
…④
-μmg?2L=
(m+M)
-
m
μ=0.3…⑤
(2)A运动到B的过程中,B做匀加速运动.
m(v0-v1)=MV1…⑥
s1=
t1…⑦
t1=2(2-
)
=0.29s
t′1=2(2+
)
=1.7s(舍去,此时V1>v1)
V1=μg
t1=0.29m/s…⑧
A与B碰撞的过程中mv1+MV1=mv1+MV2…⑨
AB碰撞后B做匀减速运动,
A到达B的左端时经历时间为t2-μ
gt2=Mv-MV2…⑩
t2=0.71s
B对地的图线如图所示.
答:(1)木块A与木板B间的动摩擦因数为0.3.
(2)如图所示.
木块A运动到B的右端时速度为v1,木板B的速度为V1,木板发生位移为s1,μmgs1=
| 1 |
| 2 |
| V | 2 1 |
-μmg(s1+L)=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 0 |
木块A与B碰撞后速度为v2,木板B的速度为V2,A运动到B的左端时,B发生位移为s2-μmgs2=
| 1 |
| 2 |
| v | 2 |
| 1 |
| 2 |
| v | 2 2 |
μmg(s2-L)=
| 1 |
| 2 |
| v | 2 |
| 1 |
| 2 |
| v | 2 2 |
由于碰撞前后机械能守恒
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| V | 2 2 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| V | 2 1 |
-μmg?2L=
| 1 |
| 2 |
| v | 2 |
| 1 |
| 2 |
| v | 2 0 |
μ=0.3…⑤
(2)A运动到B的过程中,B做匀加速运动.
m(v0-v1)=MV1…⑥
s1=
| V1 |
| 2 |
t1=2(2-
| 2 |
| L |
| v0 |
t′1=2(2+
| 2 |
| L |
| v0 |
V1=μg
| m |
| M |
A与B碰撞的过程中mv1+MV1=mv1+MV2…⑨
|

AB碰撞后B做匀减速运动,
A到达B的左端时经历时间为t2-μ
| m |
| M |
t2=0.71s
B对地的图线如图所示.
答:(1)木块A与木板B间的动摩擦因数为0.3.
(2)如图所示.
点评:本题综合考查了动量守恒定律、动能定理、能量守恒定律、牛顿第二定律等知识,综合性较强,对学生的能力要求较高,是道难题.

练习册系列答案
相关题目
 如图(甲)所示,质量为m=50g,长l=10cm的铜棒,用长度也为l的两根轻软导线水平悬吊在竖直向上的匀强磁场中,磁感应强度B=1/3T.未通电时,轻线在竖直方向,通入恒定电流后,棒向外偏转的最大角度θ=37°,求此棒中恒定电流的大小.
如图(甲)所示,质量为m=50g,长l=10cm的铜棒,用长度也为l的两根轻软导线水平悬吊在竖直向上的匀强磁场中,磁感应强度B=1/3T.未通电时,轻线在竖直方向,通入恒定电流后,棒向外偏转的最大角度θ=37°,求此棒中恒定电流的大小. 如图(甲)所示,质量不计的弹簧竖直固定在水平面上,t=0时刻,将一金属小球从弹簧正上方某一高度处由静止释放,小球落到弹簧上压缩弹簧到最低点,然后又被弹起离开弹簧,上升到一定高度后再下落,如此反复,通过安装在弹簧下端的压力传感器,测出这一过程弹簧弹力F随时间,变化的图象如图(乙)所示,则( )
如图(甲)所示,质量不计的弹簧竖直固定在水平面上,t=0时刻,将一金属小球从弹簧正上方某一高度处由静止释放,小球落到弹簧上压缩弹簧到最低点,然后又被弹起离开弹簧,上升到一定高度后再下落,如此反复,通过安装在弹簧下端的压力传感器,测出这一过程弹簧弹力F随时间,变化的图象如图(乙)所示,则( )
 如图(甲)所示,质量m=0.5kg,初速度υ0=10m/s的物体,受到一个与初速方向相反的外力F的作用,沿粗糙的水平面滑动,经3s撤去外力,直到物体停止,整个过程物体的υ-t图象如图(乙)所示,g取10m/s2,则下列判断正确的是( )
如图(甲)所示,质量m=0.5kg,初速度υ0=10m/s的物体,受到一个与初速方向相反的外力F的作用,沿粗糙的水平面滑动,经3s撤去外力,直到物体停止,整个过程物体的υ-t图象如图(乙)所示,g取10m/s2,则下列判断正确的是( )