题目内容
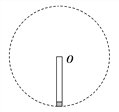
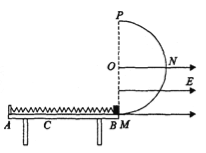
【题目】如图所示，桌面上有一轻质弹簧，左端固定在A点，自然状态时其右端B点位于桌面右侧边缘．水平桌面右侧有一竖直放置、半径R=0.3m的光滑半圆轨道MNP，桌面与轨道相切于M点．在以MP为直径的右侧和水平半径ON的下方部分有水平向右的匀强电场，场强的大小E=
．现用质量m1=0.4kg的物块将弹簧缓慢压缩到C点，释放后弹簧恢复原长时物块恰停止在B点．用同种材料、质量为m2=0.2kg、带+q的绝缘物块将弹簧缓慢压缩到C点，释放后物块离开桌面由M点沿半圆轨道运动，恰好能通过轨道的最高点P．（取g=10m/s2）求：
（1）物块m2经过桌面右侧边缘B点时的速度；
（2）物块m2在半圆轨道运动时对轨道的最大压力；
（3）释放后物块m2运动过程中克服摩擦力做的功．
【答案】（1）
；（2）
；（3）
【解析】
试题分析：解：（1）在最高点重力提供向心力，由牛顿第二定律得：
B到P的过程中重力和电场力做功，由动能定理得：
联立以上两个方程式得：。
（2）依题意，物块与圆心的连线与竖直方向之间的夹角是45°位置时（设为D点），对轨道的压力最大，物块对应的速度为
，根据动能定理得：
根据牛顿第二定律：
联立可以得到：
由牛顿第三定律得，物体对轨道的最大压力为。
（3）由功能关系得：
联立可以得克服摩擦力做功：
。
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
