题目内容
如图所示，质量mA=3.0kg的物体A和质量为mB=2.0kg的物体B紧靠着放在光滑水平面上．从某一时刻t=0起，对B施加向右的水平恒力F2=4.0N，同时对A施加向右的水平变力F1，当t=0时，F1为24N，以后每秒钟均匀减小2.0N，即F1=24-2t（N）．那么在2秒末两物体的加速度a2= m/s2； 从t=0起，经过 s时间两物体分离．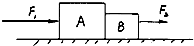
【答案】分析：当A、B恰好分离时，之间的弹力减为零，加速度相同；求解出临界加速度和此时的推力F1；最后对整体分析求解加速度．
解答：解：当A、B恰好分离时，之间的弹力减为零，加速度相同，对物体B受力分析，受重力、支持力和拉力F2，根据牛顿第二定律，有：F2=mBa，
解得：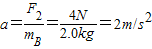
；
此时A受重力、支持力和推力F1，根据牛顿第二定律，有：F1=mAa=3×2=6N；
由于F1=24-2t（N），故t=9s；
2s时AB整体受重力、支持力、两个推力，根据牛顿第二定律，有：
F1+F2=（mA+mB）a′
解得：a′=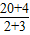
=4.8m/s2；
故答案为：4.8，9．
点评：本题关键找出恰好分离的临界状态，巧用整体法与隔离法，最后根据牛顿第二定律列式求解，不难．
解答：解：当A、B恰好分离时，之间的弹力减为零，加速度相同，对物体B受力分析，受重力、支持力和拉力F2，根据牛顿第二定律，有：F2=mBa，
解得：
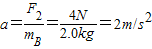；此时A受重力、支持力和推力F1，根据牛顿第二定律，有：F1=mAa=3×2=6N；
由于F1=24-2t（N），故t=9s；
2s时AB整体受重力、支持力、两个推力，根据牛顿第二定律，有：
F1+F2=（mA+mB）a′
解得：a′=
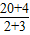=4.8m/s2；故答案为：4.8，9．
点评：本题关键找出恰好分离的临界状态，巧用整体法与隔离法，最后根据牛顿第二定律列式求解，不难．
练习册系列答案
阅读快车系列答案
相关题目
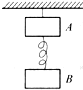如图所示，质量mA=2m、mB=3m的两物体之间用弹簧相连，弹簧的质量不计．A物体用线悬挂，使系统处于平衡状态．当悬线突然被烧断的瞬间，A物体的加速度大小是
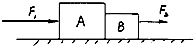如图所示，质量mA=3.0kg的物体A和质量为mB=2.0kg的物体B紧靠着放在光滑水平面上．从某一时刻t=0起，对B施加向右的水平恒力F2=4.0N，同时对A施加向右的水平变力F1，当t=0时，F1为24N，以后每秒钟均匀减小2.0N，即F1=24-2t（N）．那么在2秒末两物体的加速度a2=
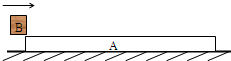如图所示，质量mA=0.9kg的长板A静止在光滑的水平面上，质量mB=0.1kg的木块B以初速v0=10m/s滑上A板，最后B木块停在A板上．求：
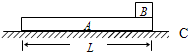如图所示，质量mA为4.0kg的木板A放在水平面C上，木板与水平面间的动摩擦因数μ为0.24，木板右端放着质量mB为1.0kg的小物块B（视为质点），它们均处于静止状态．木板突然受到水平向右的12N？s的瞬时冲量I作用开始运动，当小物块滑离木板时，木板的动能EM为8.0J，小物块的动能为0.50J，重力加速度取10m/s2，求
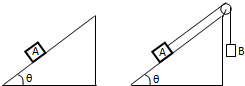如图所示，质量mA=4kg的物体A放在倾角为θ=37°的斜面上时，恰好能匀速下滑．现用细线系住物体A，并平行于斜面向上绕过光滑的定滑轮，另一端系住物体B，释放后物体A沿斜面以加速度a=2m/s2匀加速上滑．（sin37°=0.6，cos37°=0.8）求：