题目内容
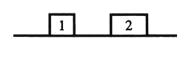
【题目】如图所示,1和2是放在水平地面上的两个小物块(可视为质点),与地面的滑动摩擦系数相同,两物块间的距离d=170.00m,它们的质量分别为m1=2.00kg、m2=3.00kg。现令它们分别以初速度v1=10.00m/s和v2=2.00m/s迎向运动,经过时间t=20.0s,两物块相碰,碰撞时间极短,碰后两者粘在一起运动。求从刚碰后到停止运动过程中损失的机械能。
【答案】ΔE=14.4J
【解析】
因两物块与地面间的滑动摩擦系数相同,故它们在摩擦力作用下加速度的大小是相同的,以a表示此加速度的大小。先假定在时间t内,两物块始终作减速运动,都未停下。现分别以s1和s2表示它们走的路程,则有
![]() (1)
(1)
![]() (2)
(2)
而s1+s2=d (3)
解(1)、(2)、(3)三式并代入有关数据得a=0.175m/s2 (4)
经过时间t,两物块的速度分别为v'1=v1at (5)
v'2=v2at (6)
代入有关数据得v'1=6.5m/s (7)
v'2=1.5m/s (8)
v'2为负值是不合理的,因为物块是在摩擦力作用下作减速运动,当速度减少至零时,摩擦力消失,加速度不复存在,v'2不可为负。v'2为负,表明物块2经历的时间小于t时已经停止运动,(2)式从而(4)、(6)、(7)、(8)式都不成立。在时间t内,物块2停止运动前滑行的路程应是
![]() (9)
(9)
解(1)、(9)、(3)式,代入有关数据得a=0.20m/s2 (10)
由(5)、(10)式求得刚要发生碰撞时物块1的速度v'1=6.0m/s (11)
而物块2的速度v'2=0 (12)
设V为两物块碰撞后的速度,由动量守恒定律有
m1v'1=(m1+m2)V (13)
刚碰后到停止运动过程中损失的机械能
![]() (14)
(14)
由(13)、(14)得
![]() (15)
(15)
代入有关数据得ΔE=14.4J (16)
评分标准:本题12分。通过定量论证得到(9)式共4分,求得(11)式得4分,(13)式1分,(14)式1分,(15)式1分,(16)式1分。

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案