题目内容
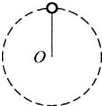 一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球在竖直平面内作半径为R的圆周运动,如图所示,则( )
一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球在竖直平面内作半径为R的圆周运动,如图所示,则( )分析:轻杆拉着小球在竖直面内做圆周运动,在最低点一定表现为拉力,在最高点可能表现为拉力,也可能表现为支持力,根据牛顿第二定律判断杆对球的作用力大小和方向.
解答:解:A、小球过最低点时,根据F-mg=m
,则F=mg+m
,知拉力大于重力,则球对杆的力一定大于球的重力.故A错误.
B、因为杆子在最高点速度小于
时,杆子表现为支持力,速度越小,支持力越大,当速度为零时,支持力和重力相等,所以小球在最高点最小速度为零.故B错误.
C、小球在最高点,当v>
,杆子对球的作用力与重力方向相同,当v<
时,杆子对球的作用力与重力方向相反.故C错误.
D、小球过最高点时,杆对球的作用力可以与球所受重力方向相反,因为合力提供向心力,合力的方向向下,则重力一定大于杆对球的作用力.故D正确.
故选D.
| v2 |
| R |
| v2 |
| R |
B、因为杆子在最高点速度小于
| gR |
C、小球在最高点,当v>
| gR |
| gR |
D、小球过最高点时,杆对球的作用力可以与球所受重力方向相反,因为合力提供向心力,合力的方向向下,则重力一定大于杆对球的作用力.故D正确.
故选D.
点评:解决本题的关键搞清向心力的来源,运用牛顿第二定律进行求解.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球做竖直平面的圆周运动,错误的是( )
| A、小球过最高点时,杆所受的弹力可以等于零 | B、小球过最高点时的最小速度为零 | C、小球过最高点时,杆对球的作用力一定与球所受重力方向相反 | D、小球过最低点时,杆对球作用力大于小球所受重力且方向相反 |
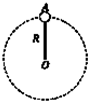 一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球在竖直面内做半径为R的圆周运动,如图所示,则下列说法正确的是( )
一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球在竖直面内做半径为R的圆周运动,如图所示,则下列说法正确的是( )| A、小球过最高点时,杆所受到的弹力可以等于零 | ||
B、小球过最高点的最小速度是
| ||
| C、小球过最高点时,杆对球的作用力一定随速度增大而增大 | ||
| D、小球过最高点时,杆对球的作用力一定随速度增大而减小 |
 如图所示,一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球做半径为R的圆周运动,以下说法正确的是( )
如图所示,一轻杆一端固定质量为m的小球,以另一端O为圆心,使小球做半径为R的圆周运动,以下说法正确的是( )