题目内容
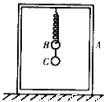
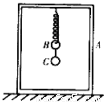
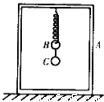
 如图所示为某课外探究小组所设计的实验装置:把一个质量为M的长方形框架A静止放在水平地面上.一个轻弹簧,上端与框架A的顶端相连,下端与质量为m的小球B相连,B的下面再通过轻质细线与小球C相连.整体处于静止状态.现剪断细线,把小球C拿走,小球B便开始上下做简谐运动.实验表明,小球C的质量存在一个临界值,超过这个临界值,当剪断细线拿走小球C后,小球承向上做简谐运动的过程中,框架A会离开地面.试求小球C的这一质量的临界值.
如图所示为某课外探究小组所设计的实验装置:把一个质量为M的长方形框架A静止放在水平地面上.一个轻弹簧,上端与框架A的顶端相连,下端与质量为m的小球B相连,B的下面再通过轻质细线与小球C相连.整体处于静止状态.现剪断细线,把小球C拿走,小球B便开始上下做简谐运动.实验表明,小球C的质量存在一个临界值,超过这个临界值,当剪断细线拿走小球C后,小球承向上做简谐运动的过程中,框架A会离开地面.试求小球C的这一质量的临界值.分析:剪断细线后,小球B做简谐运动,找出框架对地面的压力为零的临界状态,分别对直挂B、直挂BC、剪断细线三种情况下的小球、框架受力分析,根据牛顿第二定律和平衡条件列方程后联立求解.
解答:解:设小球C的质量临界值为m0,劲度系数为k,重力加速度为g;
(1)弹簧下端只挂小球B时,当B静止不动时,设弹簧伸长量为x1,对B,有:
mg=kx1 ①
(2)小球B下面再挂上C时,当B和C静止不动时,设弹簧再伸长x2,对B和C,有:
(m+m0)g=k(x1+x2) ②
(3)细线剪断,小球C拿走后,小球B运动到最高点时,框架A对地面的压力最小为零,此时设弹簧压缩量为x3,对框架A,有:
Mg=kx3 ③
根据简谐运动的对称规律,有:
x1+x3=x2(等于振幅A) ④
解得
m0=M+m
即小球C的质量的临界值为M+m.
(1)弹簧下端只挂小球B时,当B静止不动时,设弹簧伸长量为x1,对B,有:
mg=kx1 ①
(2)小球B下面再挂上C时,当B和C静止不动时,设弹簧再伸长x2,对B和C,有:
(m+m0)g=k(x1+x2) ②
(3)细线剪断,小球C拿走后,小球B运动到最高点时,框架A对地面的压力最小为零,此时设弹簧压缩量为x3,对框架A,有:
Mg=kx3 ③
根据简谐运动的对称规律,有:
x1+x3=x2(等于振幅A) ④
解得
m0=M+m
即小球C的质量的临界值为M+m.
点评:本题关键是:(1)找出临界状态;(2)简谐运动的对称性;(3)对各个平衡态受力分析列方程.

练习册系列答案
相关题目
 在电学实验中由于电压表、电流表内阻的影响,使得测量结果总存在系统误差.某校课外研究性学习小组进行了消除系统误差的探究实验,下面就举一例:
在电学实验中由于电压表、电流表内阻的影响,使得测量结果总存在系统误差.某校课外研究性学习小组进行了消除系统误差的探究实验,下面就举一例: