题目内容
2.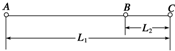 中央电视台近期推出了一个游戏节目--推矿泉水瓶.选手们从起点开始用力推瓶一段时间后,放手让瓶向前滑动,若瓶最后停在桌上有效区域内,视为成功;若瓶最后不停在有效区域内或在滑行过程中倒下均视为失败.其简化模型如图所示,AC是长度为L1=5m的水平桌面,选手们可将瓶子放在A点,从A点开始用一恒定不变的水平推力推瓶,BC为有效区域.已知BC长度为L2=1m,瓶子质量为m=0.5kg,有推力作用时的加速度为36m/s2,没有推力作用时的加速度为4m/s2,瓶子沿AC做直线运动,(g取10m/s2)假设瓶子可视为质点,那么该选手要想游戏获得成功,试问:
中央电视台近期推出了一个游戏节目--推矿泉水瓶.选手们从起点开始用力推瓶一段时间后,放手让瓶向前滑动,若瓶最后停在桌上有效区域内,视为成功;若瓶最后不停在有效区域内或在滑行过程中倒下均视为失败.其简化模型如图所示,AC是长度为L1=5m的水平桌面,选手们可将瓶子放在A点,从A点开始用一恒定不变的水平推力推瓶,BC为有效区域.已知BC长度为L2=1m,瓶子质量为m=0.5kg,有推力作用时的加速度为36m/s2,没有推力作用时的加速度为4m/s2,瓶子沿AC做直线运动,(g取10m/s2)假设瓶子可视为质点,那么该选手要想游戏获得成功,试问:(1)推力作用在瓶子上的时间最长不得超过多少?
(2)推力作用在瓶子上的距离最小为多少?
分析 (1)受力分析后,先根据牛顿第二定律求解出瓶子加速和减速时的加速度,然后根据运动学公式结合几何关系列式求解出瓶子恰好滑动到C点时推力的作用时间;
(2)瓶子恰好滑动到B点,推力的作用距离最短;根据运动学公式结合几何关系列式求解即可.
解答 解:(1)要想获得游戏成功,瓶滑到C点速度正好为0,力作用时间最长,
设最长作用时间为t1,有力作用时瓶的加速度为a1,t1时刻瓶的速度为v,
力停止后加速度为a2,由牛顿第二定律得:
F-μmg=ma1 ①μmg=ma2 ②
加速运动过程中的位移:x1=$\frac{{v}^{2}}{2{a}_{1}}$ ③
减速运动过程中的位移:x2=$\frac{{v}^{2}}{2{a}_{2}}$ ④
位移关系满足:
x1+x2=L1 ⑤
又:v=a1t1 ⑥
由以上各式解得:t1 =$\frac{1}{6}$s,
即推力作用在瓶子上的时间最长不得超过$\frac{1}{6}$s.
(2)要想游戏获得成功,瓶滑到B 点速度正好为零,力作用距离最小,
设最小距离为d,则:$\frac{v{′}^{2}}{2{a}_{1}}$+$\frac{v{′}^{2}}{2{a}_{2}}$=L1-L2 ⑦
v′2=2a1d ⑧联立解得:d=0.4m;
答:(1)推力作用在瓶子上的时间最长不得超过$\frac{1}{6}$s;
(2)推力作用在瓶子上的距离最小为0.4m.
点评 本题是一道李旭综合题,本题关键找出临界情况,求出加速度后,运用运动学公式结合几何关系列式求解.

练习册系列答案
相关题目
17.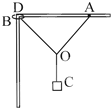 如图所示,两根等长且不可伸长的细线结于O点,A端固定在水平杆上,B端系在轻质圆环上,圆环套在竖直光滑杆上,C端挂一重物,重物质量为m.开始时用手握住轻圆环,使其紧靠D端,AD等于OA段绳长,当重物静止时如图所示.现释放圆环,圆环在竖直光滑杆上自由滑动,(运动时存在空气阻力)当重物最终静止时OA绳拉力为FA,OB绳拉力为FB,则( )
如图所示,两根等长且不可伸长的细线结于O点,A端固定在水平杆上,B端系在轻质圆环上,圆环套在竖直光滑杆上,C端挂一重物,重物质量为m.开始时用手握住轻圆环,使其紧靠D端,AD等于OA段绳长,当重物静止时如图所示.现释放圆环,圆环在竖直光滑杆上自由滑动,(运动时存在空气阻力)当重物最终静止时OA绳拉力为FA,OB绳拉力为FB,则( )
 如图所示,两根等长且不可伸长的细线结于O点,A端固定在水平杆上,B端系在轻质圆环上,圆环套在竖直光滑杆上,C端挂一重物,重物质量为m.开始时用手握住轻圆环,使其紧靠D端,AD等于OA段绳长,当重物静止时如图所示.现释放圆环,圆环在竖直光滑杆上自由滑动,(运动时存在空气阻力)当重物最终静止时OA绳拉力为FA,OB绳拉力为FB,则( )
如图所示,两根等长且不可伸长的细线结于O点,A端固定在水平杆上,B端系在轻质圆环上,圆环套在竖直光滑杆上,C端挂一重物,重物质量为m.开始时用手握住轻圆环,使其紧靠D端,AD等于OA段绳长,当重物静止时如图所示.现释放圆环,圆环在竖直光滑杆上自由滑动,(运动时存在空气阻力)当重物最终静止时OA绳拉力为FA,OB绳拉力为FB,则( )| A. | FA<mg; FB>mg | B. | FA=mg; FB=0 | C. | FA=mg; FB=mg | D. | FA>mg; FB=mg |
14.下列说法中正确的有( )
| A. | 合力一定大于分力 | |
| B. | 两个直线运动的合运动一定是直线运动 | |
| C. | 两物体间存在摩擦力,则这两物体间一定存在弹力 | |
| D. | 物体在变力的作用下一定做曲线运动 |
11.摆长为L的单摆,周期为T,若将它的摆长增加2m,周期变为2T,则L等于( )
| A. | $\frac{1}{3}$m | B. | $\frac{1}{2}$m | C. | $\frac{2}{3}$m | D. | 2m |
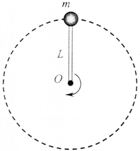 轻杆长L=60cm,一端固定于转轴O,另一端系一质量为m=0.5kg的小球,使小球在竖直平面内做圆周运动,重力加速度g=10m/s2,求:
轻杆长L=60cm,一端固定于转轴O,另一端系一质量为m=0.5kg的小球,使小球在竖直平面内做圆周运动,重力加速度g=10m/s2,求: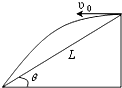 如图所示,在倾角为θ的斜面顶端,水平抛出一小钢球,恰落到斜面底端,如果斜面长为L.(忽略空气阻力)求:
如图所示,在倾角为θ的斜面顶端,水平抛出一小钢球,恰落到斜面底端,如果斜面长为L.(忽略空气阻力)求: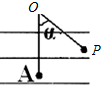 质量为m的带正电小球,电荷量为q,通过一根长为L的细线系于点O上.把细线拉直,让小球从P点由静止释放,OP连线与竖直方向的夹角为α=60°.由于水平方向电场的存在,使得小球到达竖直位置A时,速度恰好等于0.求:
质量为m的带正电小球,电荷量为q,通过一根长为L的细线系于点O上.把细线拉直,让小球从P点由静止释放,OP连线与竖直方向的夹角为α=60°.由于水平方向电场的存在,使得小球到达竖直位置A时,速度恰好等于0.求: