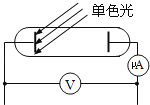
��Ŀ����
����Ŀ����ͼ��ʾ������PQ��MN�����ˮƽ��ǿ�糡��һ������������Ϊm=2.0��10��11kg�������Ϊq=+1.0��10��5C����a���ɾ�ֹ��ʼ����ѹΪU=100V�ĵ糡���ٺ�ֱ����ǿ�糡������ǿ�糡�У�������MN��ij��b��ͼ��δ�������뿪��ǿ�糡ʱ�ٶ���糡�����30��ǣ���֪PQ��MN���Ϊ20cm���������ӵ��������Բ��ƣ���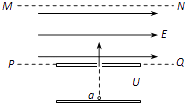
��1���������Ӹս�����ǿ�糡ʱ������v1
��2����ǿ�糡�ij�ǿ��С
��3��ab�����ĵ��Ʋ
���𰸡�
��1���⣺�����ڼ��ٵ糡���˶��Ĺ��̣��ɶ��ܶ����ã�qU= ![]()
�������ݽ�ã�v1= ![]() =
= ![]() m/s=104m/s
m/s=104m/s
�𣺴������Ӹս�����ǿ�糡ʱ������v1Ϊ104m/s��
��2���⣺���ӽ�����ǿ�糡������ƽ���˶����س��ٶȷ����������˶������У�d=v1t��
�����ص糡�������ȼ����˶������У�vy=at
������ã�tan30��= ![]()
��ţ�ٵڶ����ɵã�qE=ma��
����������ظ�ʽ���������ݵã�
E= ![]() ��103N/C=1.732��103N/C
��103N/C=1.732��103N/C
����ǿ�糡�ij�ǿ��СΪ1.732��103N/C��
��3���⣺���������̣��ɶ��ܶ����ã�
qUab= ![]() =
= ![]() ��
�� ![]() +
+ ![]() ��
��
����������ظ�ʽ���������ݵã�
Uab=400V
��b�����ĵ��Ʋ�Ϊ400V��
����������1�����������ڼ��ٵ糡�У��糡��������ΪqU�����ö��ܶ����������v1����2�����ӽ�����ǿ�糡������ƽ���˶�����ֱ������������ֱ���˶���ˮƽ�������ȼ���ֱ���˶�����������b���ٶȽ��зֽ⣬�����˶�ѧ��ʽ��ţ�ٵڶ�������ⳡǿ�Ĵ�С����3��������������ǿ�糡�Ĺ��̣����ö��ܶ�����ʽ���ab�����ĵ��Ʋ
�����㾫����ͨ��������ö��ܶ������ۺ�Ӧ�úʹ����������������ڵ糡�е��˶�������Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݣ��������:��Һ�Ρ��͵Ρ�������С��ȣ�����˵������ȷ�İ�ʾ���⣬һ�㶼���ܺ������������ڴ�����������ǿ�糡�����ܵ糡�����������Ǻ�������˿��������ַ�������:�������ֽⷨ;�ڵ�Ч���������������Խ����⣮