题目内容
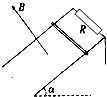如图所示，有两根和水平面成α角的光滑平行的金属导轨，相距为L，上端有一定值电阻R，下端足够长，空间有垂直于轨道平面的匀强磁场，磁感应强度为B．质量为m、电阻不计的金属杆，在轨道上由静止滑下，经过足够长的时间后，金属杆的速度达到最大速度vm，若重力加速度为g，则vm=| mgsinαR |
| B2L2 |
| mgsinαR |
| B2L2 |
| m2g2sin2αR |
| B2L2 |
| m2g2sin2αR |
| B2L2 |
分析：金属杆受重力、支持力、安培力做加速度逐渐减小的加速运动，当加速度减小到零，速度最大．根据合力为零，求出金属杆的最大的速度．根据能量守恒定律求出电阻R上消耗的功率．
解答：解：当加速度为零时，速度最大．有mgsinα=BIL，I=
．则vm=
．
当速度达到最大，做匀速运动，在此过程中能量守恒，则重力做功的功率等于整个电路消耗的功率，即电阻R上消耗的功率．有P=mgvmsinα=
．
故本题答案为：
，
．
| BLvm |
| R |
| mgsinαR |
| B2L2 |
当速度达到最大，做匀速运动，在此过程中能量守恒，则重力做功的功率等于整个电路消耗的功率，即电阻R上消耗的功率．有P=mgvmsinα=
| m2g2sin2αR |
| B2L2 |
故本题答案为：
| mgsinαR |
| B2L2 |
| m2g2sin2αR |
| B2L2 |
点评：解决本题的关键知道金属杆做加速度逐渐减小的加速运动，当加速度为零时，速度最大．根据能量守恒知，匀速运动时，重力做功的功率等于整个电路消耗的功率．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
（2013?湛江一模）如图所示，在一根粗糙的水平直杆上，套有两个质量均为m的铁环，两铁环上系着两根等长线共同拴住质量为M的小球，两铁环与小球都处于静止状态．现想办法使得两铁环间距离AB增大一些而同时仍能保持系统平衡，则OA绳和OB绳的拉力变化情况是（ ）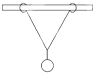
如图所示，在一根粗糙的水平直杆上套有两个质量均为m的铁环，两铁环上系着两根等长细线，共同拴住质量为M的小球，两铁环与小球组成的系统处于静止状态．现想办法使得两铁环间距离增大稍许而同时仍能保持系统平衡，则水平直杆对铁环的支持力FN和摩擦力Ff的可能变化是（ ）
