题目内容
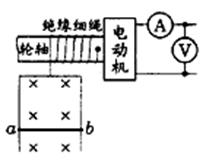
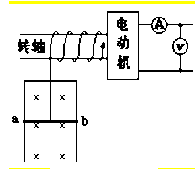
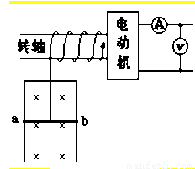
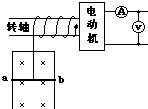 如图所示,电动机通过其转轴上的绝缘细绳竖直向上牵引一根原来静止的长为L=1m、质量m=O.1㎏的导体棒ab,导体棒紧贴在竖直放置、电阻不计的金属框架上,导体棒的电阻R=1Ω,磁感强度B=1T的匀强磁场方向垂直于导体框架所在平面,当导体棒在电动机牵引下上升h=3.8m时,获得稳定速度,此过程导体棒产生热量Q=2J.电动机工作时,输出功率P=6W恒定,不计一切摩擦,求:
如图所示,电动机通过其转轴上的绝缘细绳竖直向上牵引一根原来静止的长为L=1m、质量m=O.1㎏的导体棒ab,导体棒紧贴在竖直放置、电阻不计的金属框架上,导体棒的电阻R=1Ω,磁感强度B=1T的匀强磁场方向垂直于导体框架所在平面,当导体棒在电动机牵引下上升h=3.8m时,获得稳定速度,此过程导体棒产生热量Q=2J.电动机工作时,输出功率P=6W恒定,不计一切摩擦,求:(1)导体棒所达到的稳定速度是多少?
(2)导体棒从静止到达稳定速度的时间是多少?
分析:(1)导体棒在电动机牵引力的作用下,先做加速度减小的加速度运动,后做匀速运动,达到稳定状态,此时棒受力平衡,即绳的牵引力与重力、安培力平衡.根据电动机的输出功率和平衡条件求解
(2)根据能量守恒定律列式P出t=mgh+
mv2+Q,求出时间t.
(2)根据能量守恒定律列式P出t=mgh+
| 1 |
| 2 |
解答:解:(1)导体棒在电动机牵引力的作用下,先做加速度减小的加速度运动,后做匀速运动,达到稳定状态,此时棒受力平衡,即绳的牵引力与重力、安培力平衡.
导体棒匀速运动时,合力为零:T-mg-F=0,
其中:T=
,F=BIL,I=
,E=BLv,
化简并代入数据得:v2+v-6=0,
v=2m/s.
(2)此过程时间为t,由能量守恒定律得
P出t=mgh+
mv2+Q,
代入数据得t=1s.
答:(1)导体棒达到稳定时的速度为2m/s.
(2)导体棒从静止到达稳定速度所需要的时间是1s.
导体棒匀速运动时,合力为零:T-mg-F=0,
其中:T=
| P |
| v |
| E |
| R |
化简并代入数据得:v2+v-6=0,
v=2m/s.
(2)此过程时间为t,由能量守恒定律得
P出t=mgh+
| 1 |
| 2 |
代入数据得t=1s.
答:(1)导体棒达到稳定时的速度为2m/s.
(2)导体棒从静止到达稳定速度所需要的时间是1s.
点评:本题是电磁感应与电路知识、力学知识的综合,棒运动情况与汽车额定功率起动类似,要有联想能力.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
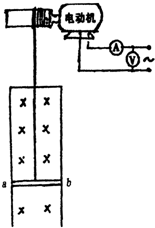 (2004?连云港模拟)如图所示,电动机通过其转轴上的绝缘细绳牵引一根原来静止的长为l=2m、质量为m=4kg的导体棒ab,导体棒贴在竖直放置、电阻不计的金属框架上,导体棒的电阻R=0.4Ω.磁感强度B=0.5T的匀强磁场方向垂直金属框架所在平面.当导体棒在电动机牵引下获得稳定速度时,电动机电路上的电压表、电流表的读数分别为220V、1A,电动机线圈电阻为20Ω,不计摩擦,g取10m/s2,求:
(2004?连云港模拟)如图所示,电动机通过其转轴上的绝缘细绳牵引一根原来静止的长为l=2m、质量为m=4kg的导体棒ab,导体棒贴在竖直放置、电阻不计的金属框架上,导体棒的电阻R=0.4Ω.磁感强度B=0.5T的匀强磁场方向垂直金属框架所在平面.当导体棒在电动机牵引下获得稳定速度时,电动机电路上的电压表、电流表的读数分别为220V、1A,电动机线圈电阻为20Ω,不计摩擦,g取10m/s2,求: