题目内容
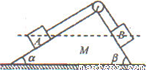
如图所示,一个上表面绝缘、质量为mA=1kg的不带电小车A置于光滑的水平面上,其左端放置一质量为mB=0.5kg、带电量为q=1.0×10-2C的空盒B,左端开口.小车上表面与水平桌面相平,桌面上水平放置着一轻质弹簧,弹簧左端固定,质量为mC=0.5kg的不带电绝缘小物块C置于桌面上O点并与弹簧的右端接触,此时弹簧处于原长,现用水平向左的推力将C缓慢推至M点(弹簧仍在弹性限度内)时,推力做的功为WF=6J,撤去推力后,C沿桌面滑到小车上的空盒B内并与其右壁相碰,碰撞时间极短且碰后C与B粘在一起.在桌面右方区域有一方向向左的水平匀强电场,电场强度大小为E=1×102N/m,电场作用一段时间后突然消失,小车正好停止,货物刚好到达小车的最右端.已知物块C与桌面间动摩擦因数μ1=0.4,空盒B与小车间的动摩擦因数μ2=0.1,OM间距s1=5cm,O点离桌子边沿N点距离s2=90cm,物块、空盒体积大小不计,g取10m/s2.求:
(1)物块C与空盒B碰后瞬间的速度v;
(2)小车的长度L;
(3)电场作用的时间t.
【答案】分析:(1)对物块C由O→M→N应用动能定理,求出C运动到N点速度,C与空盒B右壁相碰,动量守恒,根据动量守恒定律即可秋求解;
(2)C与B碰后可看作一整体,根据牛顿第二定律求出BC整体和小车的加速度,根据运动学基本公式求出小车和BC整体的位移,位移只差即为小车的长度;
(3)由题意及上问知速度相等后BC与小车以共同加速度一起做匀减速运动,最终速度为零,求出共同速度和加速度,求出运动时间即可求解.
解答:解:(1)对物块C由O→M→N应用动能定理,设C运动到N点速度大小为v得:
WF-μ1mcg(2s1+s2)= mcv2
mcv2
解得:v=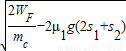 =4m/s
=4m/s
C与空盒B右壁相碰,动量守恒:mcv=(mc+mB)v
解得:v=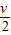 =2m/s
=2m/s
(2)C与B碰后可看作一整体,令m=mc+mB=1kg,则BC整体和小车加速度分别为:
a1=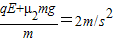 ;a2=
;a2=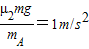
设经过t1时间后B与C整体与小车A速度相等,此过程中二者位移分别为x1、x2,以后二者相对静止.
v-a1t1=a2t1
解得:t1=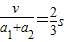
x1=vt1- a1t12=
a1t12=
x2= a2t12=
a2t12=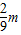
故小车长度为:L=x1-x2=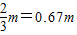
(3)由题意及上问知速度相等后BC与小车以共同加速度一起做匀减速运动,最终速度为零,
v共=a2t1=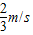 ;
;
a共=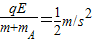
运动的时间为:t2=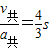
故电场作用的时间为t=t1+t2=2s
答:(1)物块C与空盒B碰后瞬间的速度为2m/s;
(2)小车的长度为0.67m;
(3)电场作用的时间为2s.
点评:本题主要考查了动量守恒定律、动能定理、运动学基本公式的直接应用,要求同学们能正确分析物体的受力情况和运动情况,难度适中.
(2)C与B碰后可看作一整体,根据牛顿第二定律求出BC整体和小车的加速度,根据运动学基本公式求出小车和BC整体的位移,位移只差即为小车的长度;
(3)由题意及上问知速度相等后BC与小车以共同加速度一起做匀减速运动,最终速度为零,求出共同速度和加速度,求出运动时间即可求解.
解答:解:(1)对物块C由O→M→N应用动能定理,设C运动到N点速度大小为v得:
WF-μ1mcg(2s1+s2)=
 mcv2
mcv2解得:v=
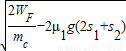 =4m/s
=4m/sC与空盒B右壁相碰,动量守恒:mcv=(mc+mB)v
解得:v=
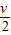 =2m/s
=2m/s(2)C与B碰后可看作一整体,令m=mc+mB=1kg,则BC整体和小车加速度分别为:
a1=
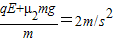 ;a2=
;a2=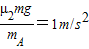
设经过t1时间后B与C整体与小车A速度相等,此过程中二者位移分别为x1、x2,以后二者相对静止.
v-a1t1=a2t1
解得:t1=
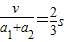
x1=vt1-
 a1t12=
a1t12=
x2=
 a2t12=
a2t12=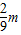
故小车长度为:L=x1-x2=
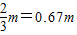
(3)由题意及上问知速度相等后BC与小车以共同加速度一起做匀减速运动,最终速度为零,
v共=a2t1=
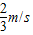 ;
;a共=
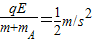
运动的时间为:t2=
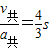
故电场作用的时间为t=t1+t2=2s
答:(1)物块C与空盒B碰后瞬间的速度为2m/s;
(2)小车的长度为0.67m;
(3)电场作用的时间为2s.
点评:本题主要考查了动量守恒定律、动能定理、运动学基本公式的直接应用,要求同学们能正确分析物体的受力情况和运动情况,难度适中.

练习册系列答案
相关题目

 的不带电小车A置于光滑的水平面上,其左端放置一质量为
的不带电小车A置于光滑的水平面上,其左端放置一质量为 、带电量为
、带电量为 的空盒B,左端开口。小车上表面与水平桌面相平,桌面上水平放置着一轻质弹簧,弹簧左端固定,质量为
的空盒B,左端开口。小车上表面与水平桌面相平,桌面上水平放置着一轻质弹簧,弹簧左端固定,质量为 的不带电绝缘小物块C置于桌面上O点并与弹簧的右端接触,此时弹簧处于原长,现用水平向左的推力将
的不带电绝缘小物块C置于桌面上O点并与弹簧的右端接触,此时弹簧处于原长,现用水平向左的推力将 缓慢推至M点(弹簧仍在弹性限度内)时,推力做的功为
缓慢推至M点(弹簧仍在弹性限度内)时,推力做的功为 ,撤去推力后,
,撤去推力后, ,电场作用一段时间后突然消失,小车正好停止,货物刚好到达小车的最右端。已知物块C与桌面间动摩擦因数
,电场作用一段时间后突然消失,小车正好停止,货物刚好到达小车的最右端。已知物块C与桌面间动摩擦因数 ,空盒B与小车间的动摩擦因数
,空盒B与小车间的动摩擦因数 ,
, 间距
间距 ,
, 点离桌子边沿
点离桌子边沿 点距离
点距离 ,物块、空盒体积大小不计,
,物块、空盒体积大小不计, 取
取 。求:
。求:
 ;
;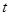 。
。
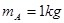 的不带电小车A置于光滑的水平面上,其左端放置一质量为
的不带电小车A置于光滑的水平面上,其左端放置一质量为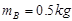 、带电量为
、带电量为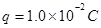 的空盒B,左端开口。小车上表面与水平桌面相平,桌面上水平放置着一轻质弹簧,弹簧左端固定,质量为
的空盒B,左端开口。小车上表面与水平桌面相平,桌面上水平放置着一轻质弹簧,弹簧左端固定,质量为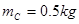 的不带电绝缘小物块C置于桌面上O点并与弹簧的右端接触,此时弹簧处于原长,现用水平向左的推力将
的不带电绝缘小物块C置于桌面上O点并与弹簧的右端接触,此时弹簧处于原长,现用水平向左的推力将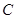 缓慢推至M点(弹簧仍在弹性限度内)时,推力做的功为
缓慢推至M点(弹簧仍在弹性限度内)时,推力做的功为 ,撤去推力后,
,撤去推力后,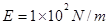 ,电场作用一段时间后突然消失,小车正好停止,货物刚好到达小车的最右端。已知物块C与桌面间动摩擦因数
,电场作用一段时间后突然消失,小车正好停止,货物刚好到达小车的最右端。已知物块C与桌面间动摩擦因数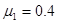 ,空盒B与小车间的动摩擦因数
,空盒B与小车间的动摩擦因数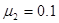 ,
,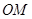 间距
间距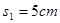 ,
,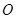 点离桌子边沿
点离桌子边沿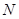 点距离
点距离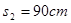 ,物块、空盒体积大小不计,
,物块、空盒体积大小不计,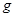 取
取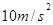 。求:
。求: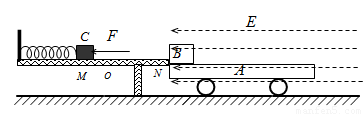
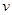 ;
;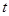 。
。