题目内容
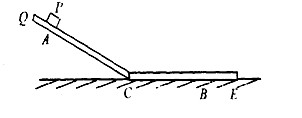
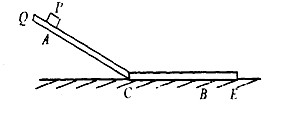
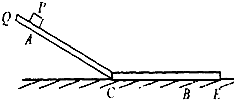某兴趣小组在研究测物块P与软垫间的动摩擦因数时，提出了一种使用刻度尺和秒表的实验方案：将软垫一部分弯折形成斜面轨道与水平轨道连接的QCE形状，并将其固定在竖直平面内，如图所示，将物块P从斜面上A处由静止释放，物块沿粗糙斜面滑下，再沿粗糙水平面运动到B处静止，设物块通过连接处C时机械能不损失，重力加速度g取l0m/s2，用秒表测得物块从A滑到B所用时间为2s，用刻度尺测得A、C间距60cm，C、B间距40cm．求：（1）物块通过C处时速度大小；
（2）物块与软垫间的动摩擦因数．
分析：根据运动学公式以及二者时间之和为2s列方程可求出C处的速度大小；
由牛顿第二定律表示出加速度的表达式，然后结合位移公式列方程求出摩擦因数．
由牛顿第二定律表示出加速度的表达式，然后结合位移公式列方程求出摩擦因数．
解答：解：（1）设物块通过C处时的速度为vc，物块由A滑到C所通过的位移为x1，时间为
，物块由C滑到B所通过的位移为x2，时间为t2．
由x=
t
得 x1=
t1 x2=
t2
且 t1+t2=2
解得：vc=1m/s
（2）由牛顿运动定律F=ma可得μmg=ma
∵vt2-v02=2ax
∴-vc2=-2ax2
解得 μ=0.125
答：（1）物块通过C处时速度大小为1m/s；
（2）物块与软垫间的动摩擦因数为0.125．
| t | 1 |
由x=
| v0+vt |
| 2 |
得 x1=
| vc |
| 2 |
| vc |
| 2 |
且 t1+t2=2
解得：vc=1m/s
（2）由牛顿运动定律F=ma可得μmg=ma
∵vt2-v02=2ax
∴-vc2=-2ax2
解得 μ=0.125
答：（1）物块通过C处时速度大小为1m/s；
（2）物块与软垫间的动摩擦因数为0.125．
点评：本题关键是利用匀变速直线运动中的公式
=
表示出AC、BC的位移，难度适中．
. |
| v |
| v0+vt |
| 2 |
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
