Question

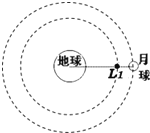
【题目】地球和月球连线上有一个拉格朗日点L1，任意位于该点的小物体在地球和月球引力的共同作用下，都可以刚好保持与地球和月球的相对位置不变，从而和月球一起以相同的周期绕地球运动，如图所示。有人想利用拉格朗日点L1的特性，在该点设一探月中转站，若以a1、a2、a3分别表示该中转站、月球和地球同步卫星绕地运转的向心加速度大小，则( )

A. a2＞a3＞a1 B. a2＞a1＞a3 C. a3＞a1＞a2 D. a3＞a2＞a1

Answer 1

【答案】D

【解析】

由题意知，空间站在L1点能与月球同步绕地球运动，其绕地球运行的周期、角速度等于月球绕地球运行的周期、角速度，由an=，分析向心加速度a1、a2的大小关系．根据分析a3与a1、a2的关系．

在拉格朗日点L1建立空间站，使其与月球同周期绕地球运动，根据向心加速度an=，由于拉格朗日点L1的轨道半径小于月球轨道半径，所以a2＞a1，同步卫星离地高度约为36000公里，故同步卫星离地距离小于拉格朗日点L1的轨道半径，根据得a3＞a2＞a1，故选D。